1. Mathematica Program for Single Transferable Vote and Ranked Choice Voting
   1. Scenario
   2. Initialization Program
   3. Flowchart
   4. Outline
   5. Program
   6. Summary and Rounds
   7. Subroutines
2. Mathematica Program for Largest Remainder
3. Mathematica Program for Highest Average

Mathematica Program for Single Transferable Vote and Ranked Choice Voting

Scenario

• Number of Seats = 5
• Candidates
  • Orange Party: O1, O2, O3, O4, O5
  • Green Party: G1, G2, G3, G4, G5
• Number of Votes = 500
• Votes for Orange Candidates = 265
• Votes for Green Candidates = 235
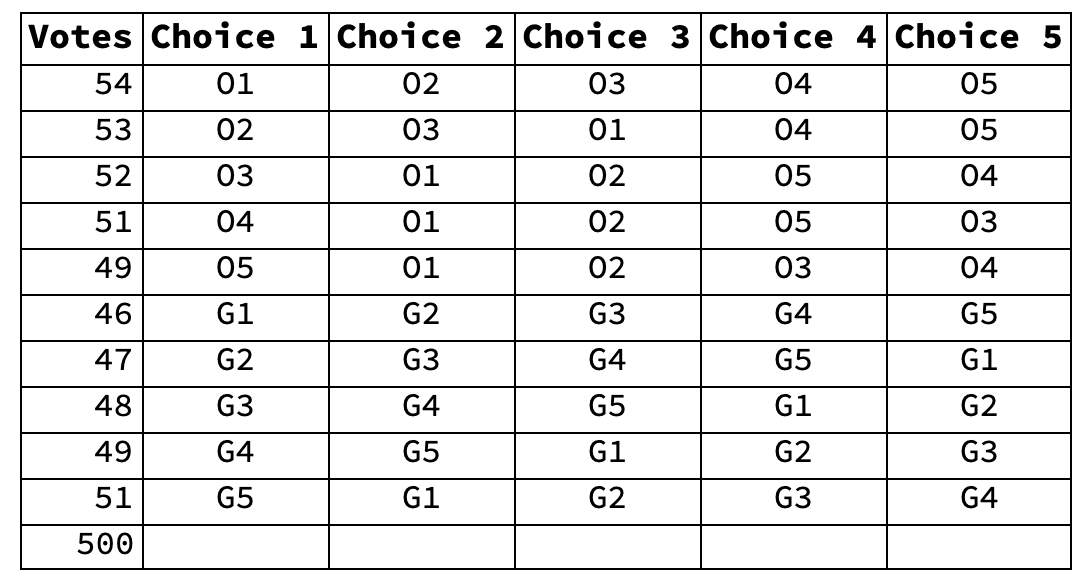
• Ballot Spreadsheet
  • 

Initialization Program

• This program
  • initializes the Ballot Spreadsheet
  • initializes the variables nbrofseats and can
  • calculates the quota

• (* Initialize Variables *)
• nbrofseats = 5; 
• (* Candidates *)
• can ={O1, O2, O3, O4, O5, G1, G2, G3, G4, G5};
• (* Initialize the Ballot Spreadsheet.
•   Columns: ballot id, votes, first choice,  second choice,  third choice,  etc
•   The number after each ballot is the number of ballots. So,  for example,  there are
•   54 ballots with preference list O1, O2, O3, O4, O5.  *)
• ballots = Join[
• Table[PadRight[{1, 1, O1, O2, O3, O4, O5}, 10], 54],
• Table[PadRight[{2, 1, O2, O3, O1, O4, O5}, 10], 53],
• Table[PadRight[{3, 1, O3, O1, O2, O5, O4}, 10], 52],
• Table[PadRight[{4, 1, O4, O1, O2, O5, O3}, 10], 51],
• Table[PadRight[{5, 1, O5, O1, O2, O3, O4}, 10], 49],
• Table[PadRight[{6, 1, G1, G2, G3, G4, G5}, 10], 46],
• Table[PadRight[{7, 1, G2, G3, G4, G5, G1}, 10], 47],
• Table[PadRight[{8, 1, G3, G4, G5, G1, G2}, 10], 48],
• Table[PadRight[{9, 1, G4, G5, G1, G2, G3}, 10], 49],
• Table[PadRight[{10, 1, G5, G1, G2, G3, G4}, 10], 51]];
• (* Calculate the Droop Quota *)
• quota = Floor[(Length[ballots]/(nbrofseats + 1))] + 1;
• (* Make the Ballot Spreadsheet the first entry in a sequence of spreadsheets *)
• ball = {ballots};

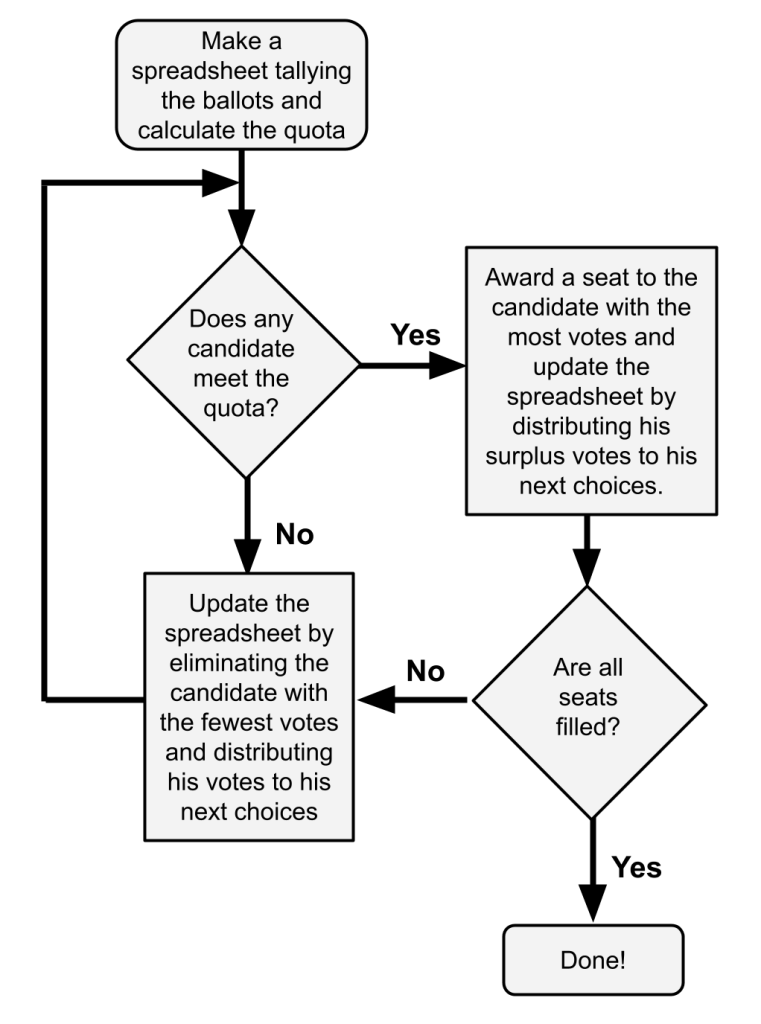
Flowchart

Outline

• (*
• Start of Program
  • Make ballot spreadsheet
  • Calculate quota
• Start of Loop
  • The program scans the Ballot Spreadsheet to see whether any candidate’s votes meet or exceed the quota.
    • If so:
      • Process Top-Vote-Getter
        • The top vote-getter wins a seat and the Ballot Spreadsheet is updated as follows:
          • The winner’s surplus votes are transferred to all his next choices.
            • (surplus votes = winner’s votes minus the quota)
          • The winner is erased from the spreadsheet.
        • The program checks whether all seats are filled.
          • If so, it goes to End of Program
          • If not, it goes to Process Lowest-Vote-Getter
    • If not:
      • Process Lowest-Vote-Getter
        • The lowest vote-getter is eliminated and the Ballot Spreadsheet is updated as follows:
          • All the eliminated loser’s votes are transferred to his next choices.
          • The loser is erased from the spreadsheet.
• End of Loop
  • Return to Start of Loop
• End of Program
  • Prints results
• *)

Program

• n=1; winner = 0; votes = 0; surplus=0; ProcessLoserY1N0 = 0;
• winnerlist = List[]; loserlist = List[]; winloss = List[];
• Do[  (* BEGIN DO LOOP  *)
  • If[Total[ball[[n]][[All,3]]]==0,Print[“No More Candidates”]; Break[]];
  • {winner,votes,surplus} = topwinner[ball[[n]],can,quota];
  • If[winner > 0, (* if winner *)
    • (* Process winner *)
    • AppendTo[winnerlist,winner];
    • AppendTo[winloss,(winner 10)];
    • balltmp1 = DistributeWinnerSurplus[ball[[n]],winner,surplus];
    • balltmp2 = EliminateCandidate[balltmp1,winner];
    • ball = Join[ball,{Null}];
    • n = n + 1;
    • balltmp3 = Select[balltmp2,#[[3]] + #[[4]] + #[[5]] + #[[6]] + #[[7]] + #[[8]] + #[[9]] + #[[10]] > 0&];
    • ball[[n]] = balltmp3;
    • If[nbrofseats == Length[winnerlist],
      • Print[“All Seats Filled”];
      • Break[]
      • ]; (* end if nbrofseats == *)
    • ProcessLoserY1N0 = 1;
  • , (* else if no winner  *)
    • ProcessLoserY1N0 = 1;
  • ]; (* end if winner  *) 
  • If[ProcessLoserY1N0 == 1, (* if process loser  *)
    • loser =bottomloser[ball[[n]],can,quota];
    • If[loser > 0, (* if loser > 0  *)
      • AppendTo[loserlist,loser];
      • AppendTo[winloss,(loser 10)+1];
      • balltmp1=EliminateCandidate[ball[[n]],loser];
      • balltmp2 =Select[balltmp1,#[[3]] + #[[4]] + #[[5]] + #[[6]] + #[[7]] + #[[8]] + #[[9]] + #[[10]] >0&];
      • ball = Join[ball,{Null}];
      • n = n+ 1;
      • ball[[n]] = balltmp2;
    • ];  (* end if loser > 0  *)
    • ProcessLoserY1N0 = 0;
  • ];  (* end if process loser  *)
• , {100}];  (* END DO LOOP  *)
• Print[“Winners: “, winnerlist];

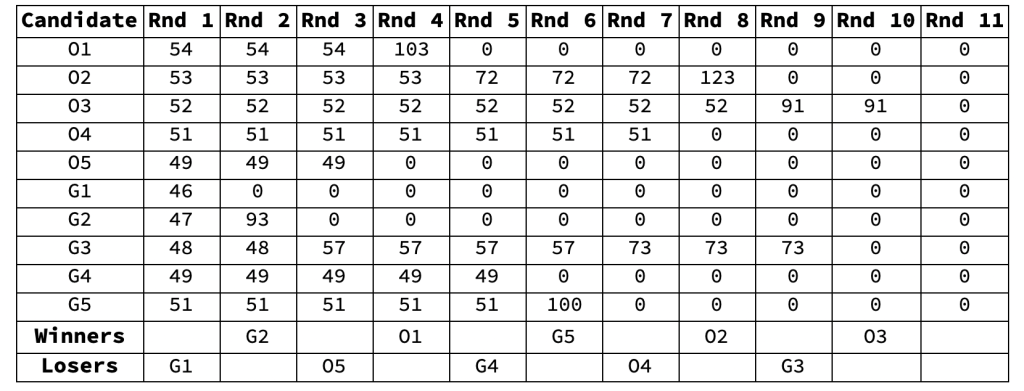
Summary and Rounds

• Number of Seats = 5
• Number of Votes = 500
• Candidates
  • Orange Party: O1, O2, O3, O4, O5,
  • Green Party : G1, G2, G3, G4, G5
• Quota = (500 / (5 + 1)) + 1 = 84
• Winners: G2, O1, G5, O2, O3

Subroutines

• Subroutine topwinner
• (*
• Winner = the top vote-getter who exceeds quota
•  plus the number of his votes and the surplus.
• Winner = 0 if no candidate exceeds quota.
• *)
• topwinner[ball_,can_,quota_] :=
• Module[{voten,winner=0,votes=0,surplus=0,topscore = 0},
• topscore = Max[Table[Total[Select[ball,#[[3]] == n&][[All,2]]],{n,can}]];
• Do[voten =Total[Select[ball,#[[3]] == n&][[All,2]]];
  • If[voten>=quota && voten >=topscore,
    • winner =n; 
    • surplus = voten-quota; 
    • votes = voten;
    • Break[]
  • ],
• {n,can}];
• {winner,votes,surplus}
• ];

• Subroutine bottomloser
• (* 
• Bottomloser = the lowest vote-getter who fails to exceed quota
• Bottomloser = 0 if no candididate fails to exceed quota 
• *)
• bottomloser[ball_,can_,quota_] :=
• Module[{voten =0,votesbycan=0,minvote=0,output = 0},
• votesbycan = List[];
• Do[voten =Total[Select[ball,#[[3]] == n&][[All,2]]];
  • If[voten >0,AppendTo[votesbycan,{n,voten}]],
• {n,can}];
• minvote = Min[votesbycan[[All,2]]];
• If[minvote>quota,output = 0,
• output =First[Select[votesbycan,#[[2]] == minvote&][[All,1]]];
• output]]

• Subroutine EliminateCandidate
• (*
• Subroutine eliminates can2del from the ballot spreadsheet  
• *)
• EliminateCandidate[ball_,can2del_] :=
• Module[{balltmp = List[],pre,core,pos,output},
• If[can2del > 0, (* Begin If can2del *)
  • Do[
    • pre =Take[ball[[n]],2];
    • core =Drop[ball[[n]],2];
    • If[Length[Select[core,#==can2del&]] >0, (* Begin if length *)
      • pos =Extract[{1}][Flatten[Position[core,can2del]]];
      • core =Join[Take[core,pos-1],Take[core,pos-Length[core]],{0}];
    • ];   (* End if length *)
    • AppendTo[balltmp,Join[pre,core]],
  • {n,Length[ball]}];  (* End Do Loop *)
  • output =balltmp 
• , (* Else if can2del  > 0 *)
  • output = ball]
• ;(* End if can2del  > 0 *)
• output  
• ];

• Subroutine DistributeWinnerSurplus
• (*
• Subroutine distributes winner’s surplus votes to next choices 
• *)
• DistributeWinnerSurplus[ball_,winner_,surplus_] :=
• Module[{record=0,newrecords,multiplier=0},
• multiplier =N[surplus/Total[Select[ball,#[[3]] == winner&][[All,2]]]];
• newrecords = List[];
• Do[
  • record =Select[ball,#[[3]] == winner&][[r]];
  • record[[2]] = record[[2 ]]multiplier;
  • AppendTo[newrecords,record],
• {r,Length[Select[ball,#[[3]] == winner&]]}]; (*  Do End *)
• Join[newrecords, Select[ball,#[[3]] != winner&]]
• ]

Mathematica Program for Largest Remainder

• (* Number of Seats *)
  • nbrofseats = 10;
• (* Election results for candidates 1, 2, 3, … *)
  • can = { {1,463,0,0},{2, 426, 0,0},{3,111,0,0}};
    • (* Format of can ={candidate id,votes,seats, remainder} *)
• (* Constants indicating locations of fields in can brackets *)
  • fid = 1; fvotes = 2; fseats = 3; fdec = 4;
• totalvotes = Total[can[[All,fvotes]]];
• quota = totalvotes/nbrofseats;
• nbrofparties = Length[can];
• (* Calculate number of seats for each party and remainder *)
  • Do[
    • can[[n,fseats]]=QuotientRemainder[can[[n,fvotes]],quota][[1]];
    • can[[n,fdec]]=N[QuotientRemainder[can[[n,fvotes]],quota][[2]]],
    • {n,nbrofparties}];
• (* Calculate remaining number of seats to be filled *)
  • seatsneeded =nbrofseats- Total[can[[All,fseats]]];
• (* Add remaining seats to parties with highest remainders *)
  • can = ReverseSortBy[can,Last];
  • Do[
    • can[[n,fseats]] +=1,
    • {n,seatsneeded}];
    • can = SortBy[can,First];
• (* Print results *)
  • Do[
  • Print[“Party “,can[[n,fid]], “: “, can[[n,fseats]],” seats”],
  • {n,nbrofparties}];
  • Print[“Total  : “,Total[can[[All,fseats]]],” seats” ];
    • Party 1: 5 seats
    • Party 2: 4 seats
    • Party 3: 1 seats
    • Total  : 10 seats

Mathematica Program for Highest Average

• (* Number of seats *)
  • nbrofseats = 10;
• (* Election results for candidates 1, 2, 3, … *)
  • can = { {1, 463, 463, 0}, {2, 426, 426, 0}, {3, 111, 111, 0}};
    •  (* Can data items = {party identifier, number of votes, running score, number of seats}*)
• (* Constants indicating the location of data items within the can brackets *)
  • fid = 1; fvotes = 2; fscore = 3; fseats = 4;
• nbrofparties = Length[can];
• (* Set method to 1 for D’Hondt or 2 for Sainte-Lague  *)
  • method = 1;
  • (* Print[“Round “,0 ,”: “,can]*)
• (* Loop through the rounds, one at a time *)
  • Do[
  •  (* Quit if all seats have been filled *)
    •  If[Total[can[[All, fseats]]] == nbrofseats, Goto[end]];
  •  (* Find the (first) winner of the current round *)
    •  id = First[Select[can, #[[fscore]] == Max[can[[All, fscore]]] &]][[1]];
  •  (* Increment the winner’s total seats *)
    •  can[[id, fseats]] += 1;
  •  (* Compute the winner’s score for the next round *)
    •  can[[id, fscore]] =  N[can[[id, fvotes]]/( method  can[[id, fseats]] + 1)];
  •  (* Print[“Round “,n ,”: “,can];*)
  •  Label[end],
  •  {n, nbrofseats}]
• (* Print Results *)
  • Do[
  •   Print[“Party “, can[[n, fid]], “: “, can[[n, fseats]], ” seats”],
  •   {n, nbrofparties}];
  • Print[“Total  : “, Total[can[[All, fseats]]], ” seats” ];
    • Party 1: 5 seats
    • Party 2: 4 seats
    • Party 3: 1 seats
    • Total  : 10 seats