Back to Special Relativity

Contents

1. Principle of Length Contraction
2. Example
3. A Puzzlement
4. Spacetime Diagram of Length Contraction
5. Derivation of Length Contraction from the Lorentz Transformation

Principle of Length Contraction

• Δx′ = Δx/γ, where
  • γ is the Lorentz Factor
    • γ = 1 /√ (1 – v²/c²)
  • Δx is the length of an object in an inertial reference frame S in which it’s at rest
  • Δx′ is the length of the object in a reference frame in uniform motion relative to S and the length is measured by measuring the locations of the ends of the object simultaneously.
• The Principle of Length Contraction follows from the Lorentz Transformations. See derivation below.

Example

• A spacecraft is 100 meters long, measured in its rest frame by laying out a series of meter sticks end-to-end.
• The spacecraft travels at 80 percent the speed of light in Earth’s reference frame. And its length is measured by laying out a series of synchronized clocks every meter along the spaceship’s path. The clocks record when the ends of the spacecraft, fore and aft, pass by. In this way the locations of the frontend and backend of the spacecraft are measured simultaneously. The length of the spacecraft is the difference between the two measurements.
• Special Relativity predicts that the length of the spacecraft is 60 meters in Earth’s frame.
  • Δx′ = Δx / γ
  • Δx′ = 100 / (5/3) = 60 
    • where γ = 1/√[1 – (⅘)^2] = 5/3.

A Puzzlement

• The puzzlement.
  1. If the locations of the ends of the spacecraft are measured simultaneously, then the length of the spacecraft is the difference between the measurements.
  2. The spacecraft is 100 meters long measured at rest.
  3. Therefore, the difference between the measurements can’t be less than 100 meters.
• Resolution.
  • Simultaneity is relative to reference frames. So Statement #1 needs to refer to reference frames:
    • If the locations of the ends of the spacecraft are measured simultaneously in inertial frame X, then the length of the spacecraft in frame X is the difference between the measurements.
  • Thus, simultaneous measurements in the Earth’s frame yield a length less than 100 meters in the Earth’s frame. But the simultaneous measurements in the Earth’s frame are not simultaneous in the spacecraft’s rest frame. They’re consecutive. So there’s no reason to think that the measurements in the Earth’s frame would match those in the spacecraft’s rest frame. That is, there’s no reason to think that the length of spacecraft is 100 meters in the Earth’s frame.

Spacetime Diagram of Length Contraction

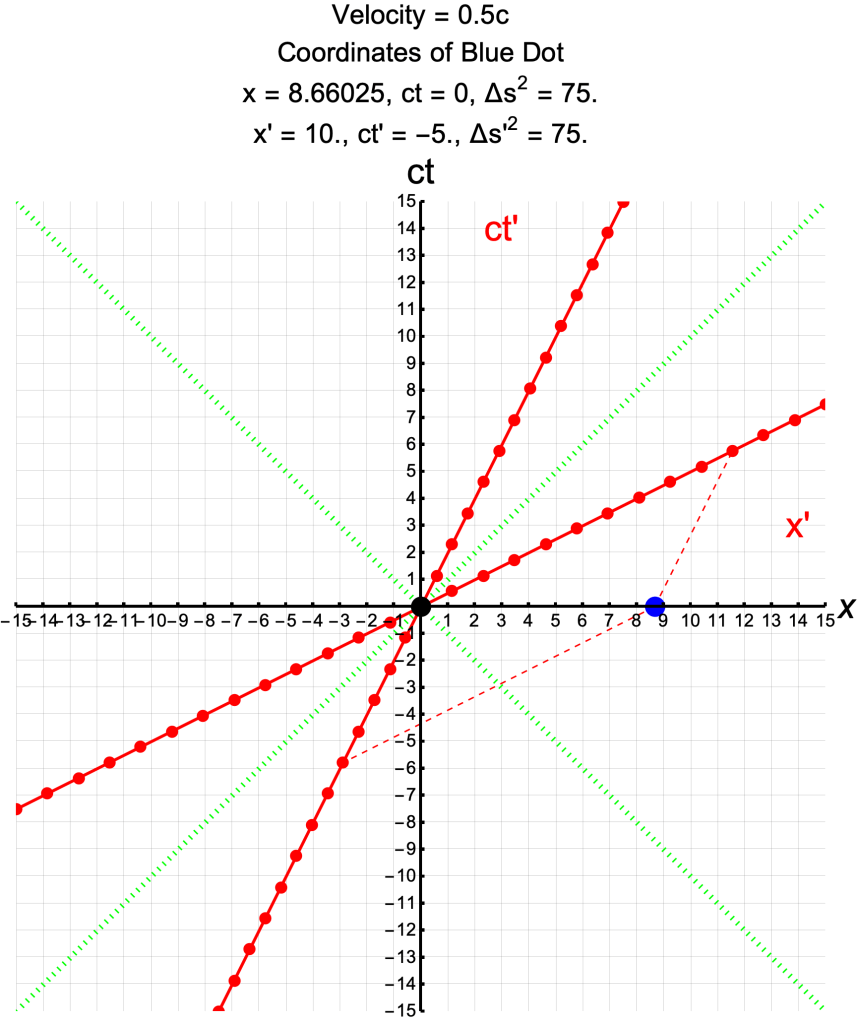
• The blue and black events are the measurements of the ends of a rod.
• The distance between the measurements is 10 meters in S′ (count the red dots) and 8.66 meters in S.
• The measurements are simultaneous in S (at ct = 0).

Derivation of Length Contraction from the Lorentz Transformation

• 1. Δt′ = γ(Δt – vΔx/c²)
  • Lorentz Transformation for time interval
• 2. Δx′ = γ(Δx – vΔt)
  • Lorentz Transformation for distance
• 3. 0 = γ(Δt – vΔx)/c²)
  • From 1 because measurements of the ends of the moving object are simultaneous in the primed frame
• 4. γΔt = vγΔx/c²
  • Expanding and rearranging 3
• 5. Δx′ = -vγΔt + γΔx
  • Expanding and rearranging 2
• 6. Δx′ = -v(vγΔx)/c² + γΔx
  • Replacing γΔt in 5 with (vγΔx)/c² using identity 4
• 7. Δx′ = γ(1 – v²/c²)Δx
  • Expanding and rearranging 6 (using Mathematica)
    • Simplify[Δxp == -v (v γ Δx)/ c^2 + γ Δx]
    • Δxp == (1 – v^2/c^2) γ Δx
• 8. γ = 1 /√ (1 – v²/c²)
  • Lorentz Factor
• 9. 1/γ² = 1 – v²/c²
  • Squaring and inverting both sides of 8
• 10. Δx′ = γ/γ² Δx
  • Replacing (1-v²/c²) in 7 with 1/γ² using identity 9
• 11. Δx′ = Δx/γ
  • From 10 since γ/γ² = 1/γ