Lorentz Transformations

Back to Special Relativity

Contents

Transformations

Suppose that the origins of the coordinate systems of two inertial reference frames are at different locations. If the reference frames are not moving relative to each other, then distances, lengths, and intervals of time are the same in both frames.
But things change when frames are in relative motion.
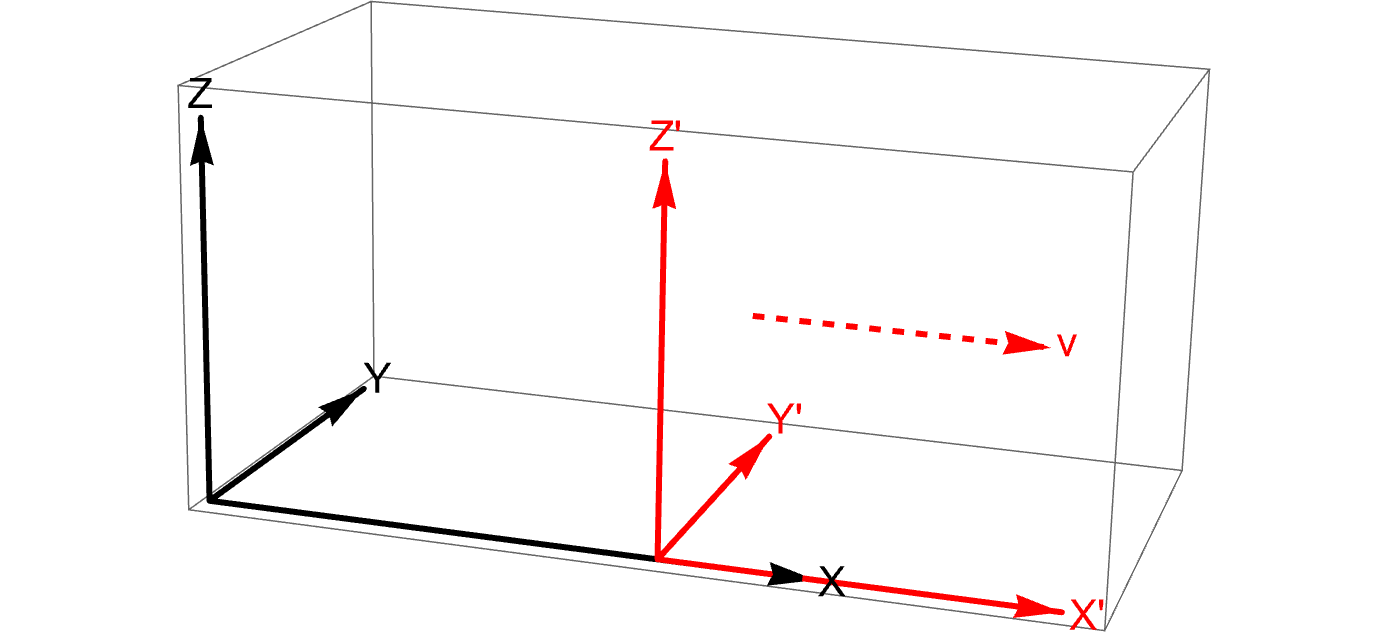
Let S′ and S be inertial reference frames with coordinates t′, x′, y′, z′ and t, x, y, z respectively such that
- their origins coincide at time zero, i.e. x′ = x = 0, y′ = y = 0, and z′ = z = 0 when t′ = t = 0
- axes x′ and x are the same line
- axes y′ and z′ are parallel to axes y and z
- the origin of S′ moves with constant velocity v in the positive direction along the x-axis of S.
It was an assumption of Classical Mechanics that distances, lengths, and intervals of time are the same in moving frames, just as they are in stationary frames. The assumption follows from the Galilean Transformations, which map unprimed coordinates to primed coordinates:
- t′ = t
- x′ = x – vt
- y′ = y
- z′ = z
It was also assumed that the velocity of an object (along the x-axis) is not the same in S and S′. Which makes sense. The origin of S′, for example, is at rest in S′ but moves with velocity v in S. For Einstein, however, there was one velocity which was the same in both S and S′: the velocity of light. From which Einstein derived the Lorentz Transformations:
- t′ = γ(t – vx/c²)
- x′ = γ(x – vt)
- y′ = y
- z′ = z
  - where γ = 1/√(1 – v²/c²).

The parameter γ (gamma), called the Lorentz Factor, is a multiplier that equals 1 when v = 0 and increases very slowly as v increases. Thus, where v is 10, 80 and 99 percent of the speed of light, γ is 1.005, 1.67, and 7.09 respectively.
The equation x′ = γ(x – vt) is like the Galilean transformation x′ = x – vt except for the γ multiplier.
The equation t′ = γ(t – vx/c²) is more cryptic. Since x′ = γ(x – vt) is the result of multiplying its Galilean counterpart by γ, it might be thought, by analogy, that the equation for time should be t′ = γt. Which is half right. The other half is -γvx/c², a seemingly small adjustment that makes space and time into spacetime.

Variants of the Lorentz Transformations

Inverse Form

The standard Lorentz transformations translate coordinates from frame S to S′, where S′ moves with velocity v relative to S. The inverse Lorentz transformations translate coordinates from S′ to S, where S moves with velocity -v relative to S′.
- t = γ(t′ + vx′/c²)
- x = γ(x′ + vt′)
- y = y′
- z = z′
  - where γ = 1/√(1 – v²/c²)
The inverse transformations are obtained from the standard transformations by replacing v with -v and solving for the unprimed variable.

Interval Form

The Interval Transformations translate intervals of time and segments of space rather than instants of time and points of space.
- Δt′ = γ(Δt – vΔx/c²)
- Δx′ = γ(Δx – vΔt)
- Δy′ = Δy
- Δz′ = Δz
  - where γ = 1/√(1 – v²/c²)
Example (time dilation):
- If S′ moves relative to S at velocity v = 0.8c, then if Δt = 2 and Δx = 0, Δt′ = 3.3

Endpoint Form

Instead of using Δ, subscripted Lorentz variables can be used for the endpoints of intervals.
- t₁′ = γ(t₁ – vx₁/c²)
- t₂′ = γ(t₂ – vx₂/c²)
- x₁′ = γ(x₁ – v₁t)
- x₂′ = γ(x₂ – vt₂)
  - where γ = 1/√(1 – v²/c²)
Example (time dilation):
- If S′ moves relative to S at velocity v = 0.8c, then if t₁ = 0, t₂ = 2, and x₁= x₂, then t₁′ = 0 and t₂′ = 3.3.

Differential Form

The differential form replaces Δs with differentials (“infinitely” small changes in variables).
- dt′ = γ(dt − (v/c²)dx)
- dx′ = γ(dx − vdt)
- dy′ = dy
- dz′ = dz
  - where γ = 1/√(1 – v²/c²)

Addition of Velocities

The Relativistic Principle of the Addition of Velocities:
- If an object (or particle or whatever) moves with velocity u′ in frame S′ in a given direction and frame S′ moves with velocity v in the same direction relative to frame S, then the object moves with velocity u in frame S in that direction, where:
  - u = (u′ + v) / (1 + vu′/c²)
Thus if an object moves at 300 m/s in frame S′ and frame S′ moves at 100 m/s relative to S then the object moves at 300 + 100 = 400 m/s in S.
But if an object moves at 0.8 c in frame S′ and frame S′ moves at 0.9 c relative to S then the object moves at 0.988372 c in S.
- Simplify[(u′ + v)/(1 + (u′ v)/c^2) /. {u′ → 0.8 c, v → 0.9 c}]
  - = 0.988372 c
Mathematica proof of Addition of Velocities:
- (Simplify[(dx+v dt)/dt] /. dx/dt → u′) / (Simplify[(dt+((v dx)/c²))/dt] /. dx/dt → u′)
  - = (u′ + v)/(1 + (u′ v)/c²)
It’s a logical consequence of u = (u′ + v) / (1 + vu′/c²) that if u′ = c then u = c.
- Mathematica
  - Simplify[(u′ + v)/(1 + (u′ v)/c²) /. u′ → c]
    - = c
The Relativistic Principle of the Addition of Velocities supplanted the straightforward Galilean Principle of the Addition of Velocities of Classical Mechanics:
- If an object (or particle or whatever) moves with velocity u′ in frame S′ in a given direction and frame S′ moves with velocity v in the same direction relative to frame S, then the object moves with velocity u = u′ + v in frame S in that direction.
The problem is that if an object moves at 0.8 c in frame S′ and frame S′ moves at 0.9 c relative to S then the object moves at 1.7 c in S.

Logical Connections

The Lorentz Transformations are a logical consequence of Einstein’s postulates (plus the homogeneity of space and time).
- View Derivation of the Lorentz Transformations from the Postulates.
Time dilation, length contraction, and the relativity of simultaneity are all logical consequences of the Lorentz Transformations.
Therefore, time dilation, length contraction, and the relativity of simultaneity are logical consequences of Einstein’s postulates (plus the homogeneity of space and time).

Lorentz Invariance

A quantity Q is Lorentz-invariant if Q = Q′ follows from the Lorentz Transformations.

Lorentz-invariant Quantities
- Speed of light
  - Follows from the Addition of Velocities.
- Line Element
  - ds² = -(c dt)² + dx² + dy² + dz²
  - Mathematica derivation:
    - g = 1/Sqrt[1 -v^2/c^2]
    - Simplify[-(c dt)^2 +dx^2+dy^2+dz^2 == -(c dtp)^2 + dxp^2 + dyp^2 + dzp^2 /.
      - {dtp → g(dt-((v dx)/c^2)),
      - dxp → g(dx-v dt),
      - dyp → dy,
      - dzp →dz}]
        
        = True
- Spacetime interval
  - -(c Δt)² + Δx² + Δy² + Δz²
  - Mathematica derivation:
    - Simplify[-c^2Δt^2 + Δx^2 + Δy^2 + Δz^2 = -c^2Δtp^2 + Δxp^2 + Δyp^2 + Δzp^2 /.
      - {Δxp →(Δx – Δt v) / Sqrt[1 – v^2/c^2],
      - Δtp → (Δt – (v Δx)/c^2) / Sqrt[1 – v^2/c^2],
      - Δyp → Δy,
      - Δzp → Δz} ]
        
        = True
- Proper Time Element
  - dτ² = -ds²/c²
  - Mathematica derivation:
    - g=1/Sqrt[1-v^2/c^2];
    - Simplify[-ds^2/c^2 == -dsp^2/c^2 /.
      - {ds → -(c dt)^2+dx^2+dy^2+dz^2,
      - dsp → -(c dtp)^2+dxp^2+dyp^2+dzp^2}];
    - Simplify[%/.
      - {dtp → g(dt-((v dx)/c^2)),
      - dxp → g(dx-v dt),
      - dyp → dy,
      - dzp → dz}]
        
        = True
- Mass (at rest)
Frame-relative Quantities
- Intervals of Time
  - Because of Time Dilation
- Simultaneity
  - Because of the Relativity of Simultaneity
- Distances and Lengths
  - Because of Length Contraction
- Velocity
- Electric Fields
  - An electric field can transform into a magnetic field
- Magnetic Fields
  - A magnetic field can transform into an electric field

Derivation of the Lorentz Transformations

Einstein derived the Lorentz Transformations from his postulates plus the homogeneity of space and time. What follows is a proof based on a variation of Einstein’s derivation by Valerio Faraoni in his book Special Relativity (Springer, 2013). For certain steps in the proof I include Mathematica commands for algebraic manipulation.

Premises

Principle of Relativity
- The laws of physics are true in every inertial reference frame.
Constancy of Speed of Light
- The speed of light = c in all inertial frames of reference.
Homogeneity of Space and Time
- In his derivation of the Lorentz Transformations, Einstein noted that the transformation equations “must be linear on account of the properties of homogeneity which we attribute to space and time.”
- The homogeneity of space and time is the fundamental tenet that the laws of physics are valid for every time t and every location x, y, z. Thus an experiment yields the same result (under the same conditions), whether performed today in London or a century from now on Mars.
- Homogeneity of space and time implies that the transformation equations are linear. Consider locations x = 1, 2, 3, 4, 5 in a stationary frame. Compare the linear transformation x′ = 2(x – vt) with the non-linear transformation x′ = x(x – vt). The former yields 2, 4, 6, 8, 10 (where v = 1 and t = 0) whereas the latter yields 1, 4, 9, 16, 25. Thus in the linear case the statement x = 2 is equidistant from x = 1 and x = 3 translates to the true statement x = 4 is equidistant from x = 2 and x = 6. But in the non-linear case the statement translates to the false statement x = 4 is equidistant from x = 1 and x = 9 .

Derivation

1. x′ = G(x – vt), where (a) G does not depend on either x or t, and (b) G is near 1 when v is small (in which case x′ ≈ x – vt).
- The Homogeneity of Space and Time means that x′ is a linear function of the S coordinates, which implies that G depends on neither x nor t.
2. x = G(x′ + vt′)
- Line 1 by the Principle of Relativity, x = G(x′ + vt′) being the inverse of x′ = G(x – vt).
3. y′ = y
- No relative motion in the y direction
4. z′ = z
- No relative motion in the z direction
5. x = ct
- A spherical wave of light is emitted at
  - x = 0, y = 0, and z = 0 at t = 0 in S
  - x′ = 0, y′ = 0, and z′ = 0 at t′ = 0 in S′.
- So, the location of the wavefront is x = ct in S.
6. x′ = ct′
- Line 5
- The location of the spherical wavefront is x′ = ct′ in S′
7. G(x – vt) = ct′
- Replace x′ in line 1 with ct′ per line 6
8. G(ct – vt) = ct′
- Replace x in line 7 with ct per line 5
9. t′ = G(ct – tv)/c
- Solve for t′ in line 8
- Mathematica
  - Solve[G (c t – v t) == c tp, tp]
    - tp = (G (c t – t v))/c
10. t′ = G(t – (v/c)t)
- Algebraic manipulation of line 9
- Mathematica
  - Simplify[G (t – t v/c) == Expand[(G (c t – t v))/c]]
    - True
11. ct = G(x′ + vt′)
- Replace x in 2 with ct per 5
12. ct = G(ct′ + vt′)
- Replace x′ in 11 with ct′ per 6
13. ct = G(c+v)t′
- Factor out t′ in line 12
14. ct = G(c+v) G(t – (v/c)t)
- Replace t′ in 13 with G(t – (v/c)t) per 10
15. ct = (G²/c) (c+v)(c-v)t
- Algebraic manipulation of line 14
- Mathematica
  - (G²/c) (c + v) (c – v) t == Simplify[G (c + v) G (t – (v/c) t)]
    - = True
16. G= √c /√(c – v²/c)
- Solve line 15 for G
- Mathematica
  - Solve[c t == (G²/c) (c + v) (c – v) t, G]
    - G = Sqrt[c]/Sqrt[c – v²/c]
17. G = 1 /√(1 – v²/c²) = γ
- where γ is the Lorentz factor
- Algebraic manipulation of line 16
- Mathematica
  - Simplify[Sqrt[c]/Sqrt[c – v²/c] == 1/Sqrt[1 – v²/c²], Assumptions → {c > 0}]
    - = True
18. x′ = γ(x – vt)
- Replace G in 1 with γ per 17
19. x = γ(x′ + vt′)
- Replace G in 2 with γ per 17
20. x = γ(γ(x – vt) + vt′)
- Replace x′ in 19 with γ(x – vt) per 18
21. t′ = (x – γ²x + γ²vt) / γv
- Solve line 20 for t′
- Mathematica
  - Solve[x == γ (γ (x – v t) + v tp), {tp}]
    - tp = (x + t v γ² – x γ²)/(v γ)
22. t′ = x/v (1-γ²)/γ + γt
- Algebraic manipulation of line 21
- Mathematica
  - Simplify[(x – γ² x + γ² v t)/(γ v) == (x/v) (1 – γ²)/γ + γ t]
    - = True
23. (1 – γ²)/γ = -γ(v²/c²)
- Algebraic manipulation of Line 17
- Mathematica
  - Simplify[(1 – γ²)/γ == -γ (v²/c²) /. γ -> 1/Sqrt[1 – v²/c²]]
    - = True
24. t′ = γ (t – xv/c²)
- Replace (1-γ²)/γ in line 22 with -γ(v²/c²) per line 23
- Mathematica
  - Simplify[γ (t – x v/c²) == x/v (-γ (v²/c²)) + γ t]
    - = True