Back to Special Relativity
Contents
- Hermann Minkowski
- Basic Concepts
- Line Element of Minkowski Spacetime
- Spacetime Intervals
- Timelike, Spacelike, Lightlike Intervals
- Proper Time and Spacetime Intervals
- Spacetime Diagrams
- Addendum
Hermann Minkowski
- In his 1905 paper setting forth Special Relativity, Einstein focused on reference frames: the Principle of Relativity, the Constancy of the Speed of Light, and the Lorentz Transformations are all about inertial frames of reference. Realizing that Einstein’s ideas undermined the concepts of space and time of Classical Mechanics, Hermann Minkowski developed the theory of four-dimensional spacetime. In his classic 1908 lecture on the subject, Raum und Zeit, Minkowski predicted:
- “From now onwards space by itself and time by itself will recede completely to become mere shadows and only a type of union of the two will still stand independently on its own.”
- Minkowski died of appendicitis in 1909 at age 44.
Basic Concepts
- Spacetime Coordinates
- The Cartesian coordinates of spacetime are ct, x, y, and z, where
- t is in units of time
- c is the speed of light
- ct is in units of length
- (meters / second) x seconds = meters.
- The Cartesian coordinates of spacetime are ct, x, y, and z, where
- Events (Spacetime Points, World Points)
- An event is a point in space at a time.
- The Euclidean analog is a point.
- Line Element
- The line element of spacetime is the infinitesimal spacetime distance between two neighboring points. It’s the metric for calculating distances, angles, lengths, areas, and volumes in spacetime.
- ds2 = -(c dt)2 + dx2 + dy2 + dz2
- The negative term -(c dt)2 makes spacetime hyperbolic rather than Euclidean.
- -t2 + x2 = constant is an equation for a hyperbola.
- The Euclidean analog is the line element of Euclidean plane geometry: ds2 = dx2 + dy2.
- The line element of spacetime is the infinitesimal spacetime distance between two neighboring points. It’s the metric for calculating distances, angles, lengths, areas, and volumes in spacetime.
- Proper Time
- Proper time is the temporal counterpart of the line element, the spacetime interval, and the world line.
- Proper Time Element:
- dτ2 = -ds2/c2
- dτ2 is in units of time squared
- meters2/ (meters / second)2 = seconds2
- dτ2 is in units of time squared
- dτ2 = -ds2/c2
- The proper time of a spacetime interval is the spacetime interval in seconds squared rather than meters squared.
- The proper time of a world line is the the world line in seconds rather than meters. It is time (as if) measured by a clock carried along the world line.
- There is no Euclidean analog.
- The Principle of Time Dilation follows from the Proper Time Element and the Line Element.
- See derivation below.
- Spacetime Interval
- The spacetime interval Δs2 is the spacetime distance between two events:
- Δs2 = -(c Δt)2 + Δx2 + Δy2 + Δz2.
- The Euclidean analog is the distance between two points
- The spacetime interval Δs2 is the spacetime distance between two events:
- World Line
- A world line is the path of an object through spacetime (in units of length).
- The Euclidean analog is a straight or curved line segment.
- Spacetime Diagram
- A spacetime diagram is a two-dimensional plot of a world line through time (along the vertical axis) and one dimension of space (along the horizontal axis).
Line Element of Minkowski Spacetime
Line Elements
- Euclid set forth his system of plane geometry axiomatically, by deriving theorems from a set of postulates. Another way of defining a theory of geometry is by specifying a coordinate system together with a line element, i.e. the infinitesimal distance between neighboring points on a line. Using algebra, trigonometry, and calculus, the line element can then be used to calculate distances, angles, lengths, areas, and volumes.
- For example, the line element of Euclidean plane geometry in Cartesian coordinates is
- ds2 = dx2 + dy2.
- where ds, dx, and dy are differentials in units of length
- ds2 = dx2 + dy2.
- Thus, to find the length of a curved line calculus can be used to add up the little ds’s that comprise the line.
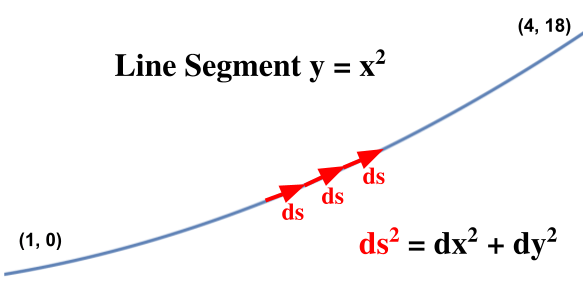
- The length of the line is 15.34 meters
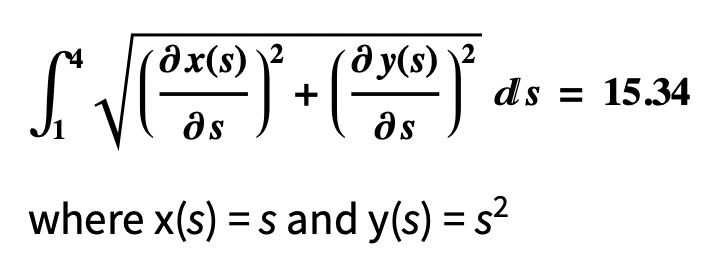
Line Element of Spacetime
- The line element of Minkowski spacetime in Cartesian coordinates is:
- ds2 = –c2dt2 + dx2 + dy2 + dz2
- where ds, dx, dy, dz, and dt are differentials, “infinitely small” changes in the variables s, x, y, z, and t.
- dx, dy, and dz are in units of distance, e.g. meters, lightyears, light-seconds.
- (c dt) is also in units of distance
- (meters / second) x seconds = meters.
- ds2 = –c2dt2 + dx2 + dy2 + dz2
- The temporal counterpart of the line element is the proper time element dτ2:
- dτ2 = -ds2/c2
- where dτ2 is in units of time squared
- (meters2) / (meters/seconds)2 = seconds2.
- where dτ2 is in units of time squared
- The proper time Δτ2 between events T and R (above) is -(-3.6 1017) / (3 108)2 = 4 seconds, making Δτ = 2 seconds.
- dτ2 = -ds2/c2
Spacetime Intervals
- In the Example involving Orange and Red Spacecraft, Orange transmits a light beam that reflects off a mirror and receives the reflection back two seconds later. Let event T be the transmission of the light beam and event R its reception.
- The elapsed time between T and R is 2 seconds in the Orange frame and 3 1/3 seconds in the Red frame.
- The distance between T and R is 0 meters in the Orange frame and 800,000,000 meters in the Red frame.
- Thus both the time interval (elapsed time) and the space interval (distance) are relative to reference frames.
- But a third kind of interval is the same in both frames, the spacetime interval:
- Δs2 = -(c Δt)2 + Δx2 + Δy2 + Δz2
- where
- Δt is the elapsed time between events
- √(Δx2 + Δy2 + Δz2) is the distance between events.
- where
- Δs2 = -(c Δt)2 + Δx2 + Δy2 + Δz2
- The spacetime interval between events T and R is -3.6 1017.
- In the Orange Frame: Δs2 = -(c Δt)2 + Δx2 = -(2 (3 108))2 + 02 = -3.6 1017.
- In the Red Frame: Δs2 = -(c Δt)2 + Δx2 = -(10/3 (3 108))2 + (8 108)2 = -3.6 1017.
- Indeed, the spacetime interval between any pair of events is the same in all inertial reference frames.
- The spacetime interval is Lorentz invariant, that is, for any inertial reference frames S and S′:
- -(c Δt)2 + Δx2 + Δy2 + Δz2 = -(c Δt′)2 + Δx′2 + Δy′2 + Δz′2
- where the primed variables of S′ result from the unprimed variables of S by the Lorentz Transformations.
- -(c Δt)2 + Δx2 + Δy2 + Δz2 = -(c Δt′)2 + Δx′2 + Δy′2 + Δz′2
- The following Mathematica command replaces the primed variables (with the prime sign replaced by the letter “p”) and affirms that the resulting identity is true:
- g = 1/Sqrt[1 – v^2/c^2];
- Simplify[-c^2 Δt^2 + Δx^2 + Δy^2 + Δz^2 == -(c Δtp)^2 + Δxp^2 + Δyp^2 + Δzp^2 /. {
- Δtp → g (Δt – ((v Δx)/c^2)),
- Δxp → g (Δx – v Δt),
- Δyp → Δy,
- Δzp → Δz}]
- = True
- The spacetime interval is Lorentz invariant, that is, for any inertial reference frames S and S′:
Timelike, Spacelike, Lightlike Intervals
- Spacetime intervals are timelike, spacelike, or lightlike according as spacetime interval Δs2 is negative, positive, or zero.
Timelike Intervals
- A spacetime interval Δs2 is timelike if it’s less than zero, that is:
- (c Δt)2 > Δx2 + Δy2 + Δz2.
- For example, for the interval between two flashes of light one second and ten meters apart:
- Δs2 = -(c Δt)2 + Δx2 = – (299792458 * 1)^2 + 10^2 = -89875517873681664 meters.
- Timelike intervals are such that:
- One event can causally affect the other.
- A particle with mass can travel between the events.
- There exists an inertial frame in which the two events occur at the same location
- Because the spacetime interval is invariant, the following is true for the example:
- -(c Δt)2 + Δx2= -89875517873681664
- where Δx = 0.
- -(c Δt)2 + Δx2= -89875517873681664
- Solving for Δt yields
- Δt = 0.9999999999999994437
- So Δx = 0 in a frame where Δs2 = -89875517873681664 and Δt = 0.9999999999999994437.
- Because the spacetime interval is invariant, the following is true for the example:
Spacelike Intervals
- A spacetime interval Δs2 is spacelike if it’s greater than zero, that is:
- Δx2 + Δy2 + Δz2 > (c Δt)2.
- For example, for the interval between two flashes light 1 second apart, one on Earth and the other on the Moon:
- Δs2 = -(c Δt)2 + Δx2 = – (299792458 * 1)^2 + 384400000^2 = 57887842126318236 meters.
- The distance from Earth to the Moon is 384,400,000 meters.
- Δs2 = -(c Δt)2 + Δx2 = – (299792458 * 1)^2 + 384400000^2 = 57887842126318236 meters.
- Spacelike intervals are such that:
- The events are too far apart for one to causally affect the other.
- A particle with mass can’t travel from one to the other.
- There exists an inertial frame in which the events are simultaneous.
- Because the spacetime interval is invariant, the following is true for the example:
- -(c Δt)2 + Δx2= 57887842126318236
- where Δt = 0.
- -(c Δt)2 + Δx2= 57887842126318236
- Solving for Δx yields
- Δx = 240598924
- So Δt = 0 in a frame where Δs2 = 57887842126318236 and Δx = 240598924.
- Because the spacetime interval is invariant, the following is true for the example:
LIghtlike Intervals
- A spacetime interval Δs2 is lightlike (or null) if it’s zero, that is:
- (c Δt)2 = Δx2 + Δy2 + Δz2
- For example, for the interval between the transmission of a pulse of light from one location and its reception at a second location 299,792,458 meters distant:
- Δs2 = -(c Δt)2 + Δx2 = -(299792458 * 1)^2 + 299792458^2 = 0 meters.
- Lightlike intervals are such that:
- Only a photon (or other massless particle) can travel between the events.
- No inertial frame exists where the events are simultaneous or occur at the same place.
- Solving -(299792458 Δt)^2 + 0^2 = 0 for Δt yields Δt = 0
- Solving -0^2 + Δx^2 = 0 for Δx yields Δx = 0.
Proper Time and Spacetime Intervals
- The elapsed time between two (instantaneous) events varies from one reference frame to another. But there is one elapsed time that’s special: the proper elapsed time. The graph shows what makes it special.
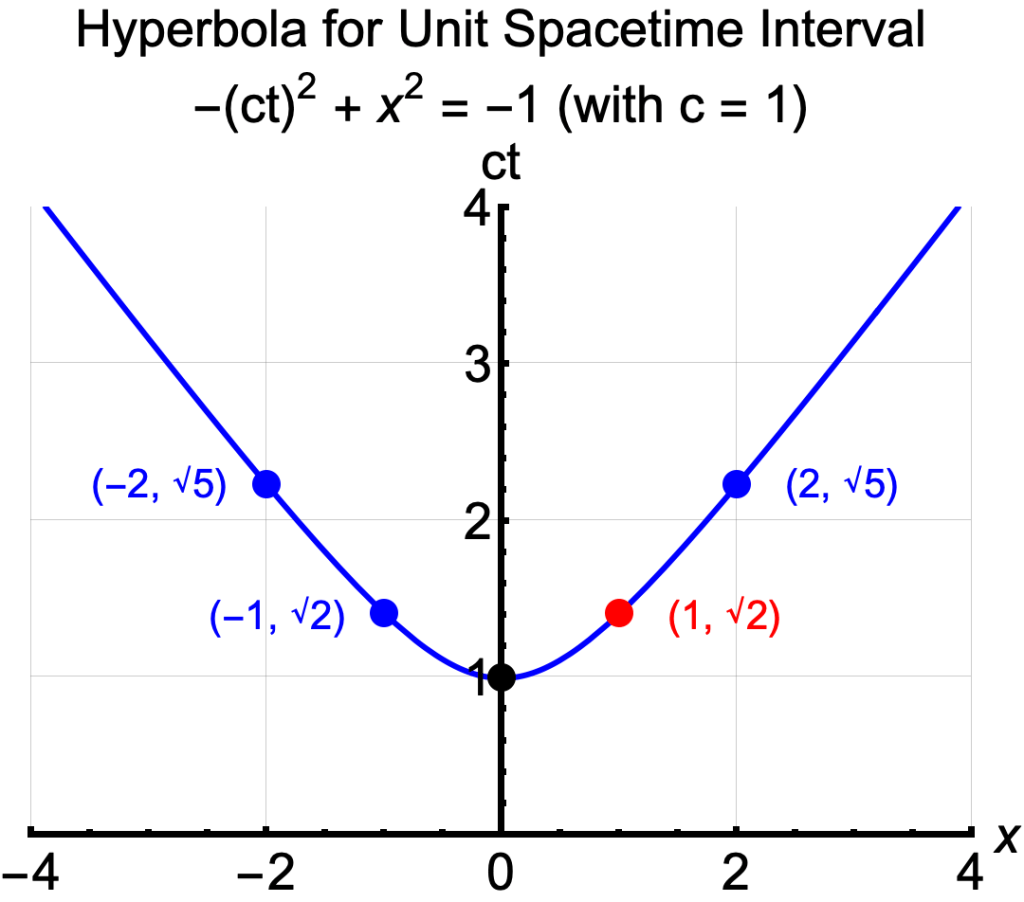
- Suppose two events in your reference frame are √2 seconds and 1 meter apart. To make things simple we’ll assume that c = 1. So the spacetime interval is -(√2)2 + 12 = -1. That’s the red dot on the graph. The blue line represents every combination of ct seconds and x meters whose spacetime interval equals -1, like yours. So for the blue dots on the graph, from left to right, we have:
- -(√5)2 + (-2)2 = -1
- -(√2)2 + (-1)2 = -1
- -(√2)2 + (1)2 = -1
- -(√5)2 + (2)2 = -1
- But there’s one dot that’s different: that’s the black dot at the bottom of the hyperbola. It’s the dot where x = 0 and ct is at its lowest point.
- -(1)2 + (0)2 = -1
- It’s the dot that defines the proper elapsed time between the events in your reference frame. By contrast, the elapsed time in your frame and in every other frame is dilated.
Spacetime Diagrams
- You can’t visualize 4-dimensional spacetime the way you can 3-dimensional space, but you can visualize 2-dimensional spacetime the way you can 2-dimensional space.
- A spacetime (or Minkowski) diagram is a neat way of visualizing spacetime, consisting of a two-dimensional graph plotting coordinate ct against coordinate x, ignoring y and z.
- A point (ct, x) on the graph represents a worldpoint, a location-at-a-time.
- A line on the graph represents a worldline, a continuous, one-dimensional path of a particle in spacetime.
- The important thing to bear in mind about spacetime diagrams is that particles move only along the x-axis.
A Basic Spacetime Diagram, in Meters


- This spacetime diagram depicts the movement of four particles along the x-axis over the course of one second.
- The horizontal x-axis represents a distance of 3 x 108 meters.
- The vertical ct-axis represents the span of one second in ct units.
- ct = 3 x 108 meters / second times t seconds = 3 x 108 meters. So t = 1 second.
- The particles:
- The green particle, a photon, traverses the x-axis from x = 0 to x = 3 x 108 as it moves through time along the ct-axis from ct = 0 to ct = 3 x 108. It thus travels 3 x 108 meters in one second, the speed of light.
- The blue and brown particles travel toward each other on the x-axix at half the speed of light, colliding at x = 1.5 x 108, i.e. at worldpoint (ct, x) =(3 x 108,1.5 x 108).
- Finally, the red particle remains at rest on the x-axis, “moving through time” from worldpoint (ct, x) = (0, 2.5 x 108) to worldpoint (ct, x) = (3 x 108, 2.5 x 108).
A Basic Spacetime Diagram, in Light-Seconds
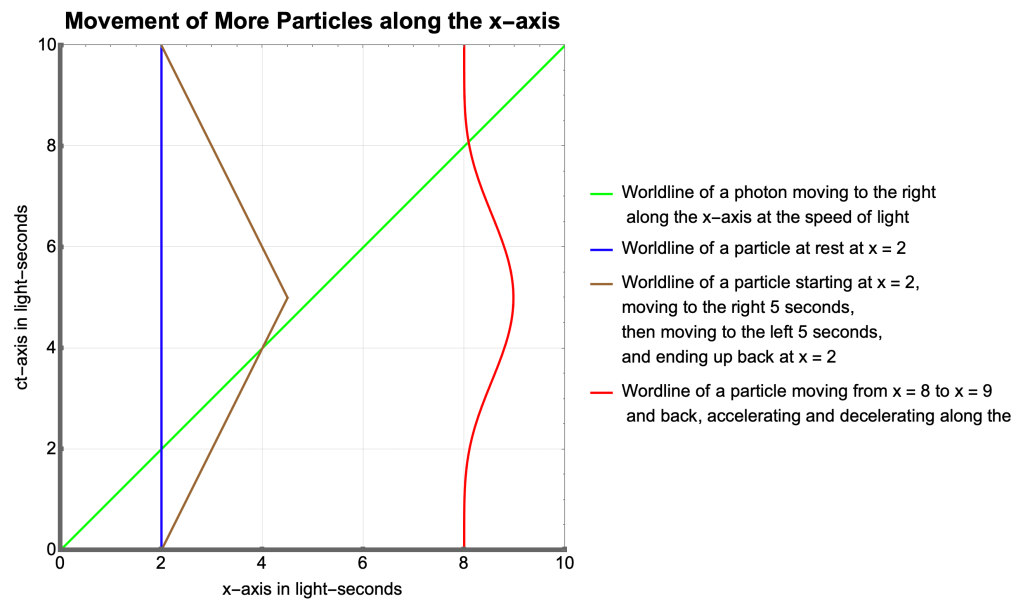
- This Spacetime Diagram uses light-seconds rather than meters.
- 1 light-second = 3 x 108 meters
- The x-axis represents 10 light-seconds of distance, that’s 30 x 108 meters
- The ct-axis represents 10 light-seconds of time, meaning 10 seconds.
- Particles
- The green photon travels 10 light-seconds in 10 seconds, at the speed of light.
- The blue particle remains fixed at x = 2
- The brown particle moves from x = 2 to x = 4.5 in the first 5 seconds and back to x = 2 in the second 5 seconds.
- The red particle moves from x = 8 to x = 9 and back, accelerating, decelerating, stopping, reversing direction, accelerating, decelerating, and finally coming to rest where it began.
Spacetime Diagrams for Frames in Relative Motion
Plotting the Axes of the Moving Frame
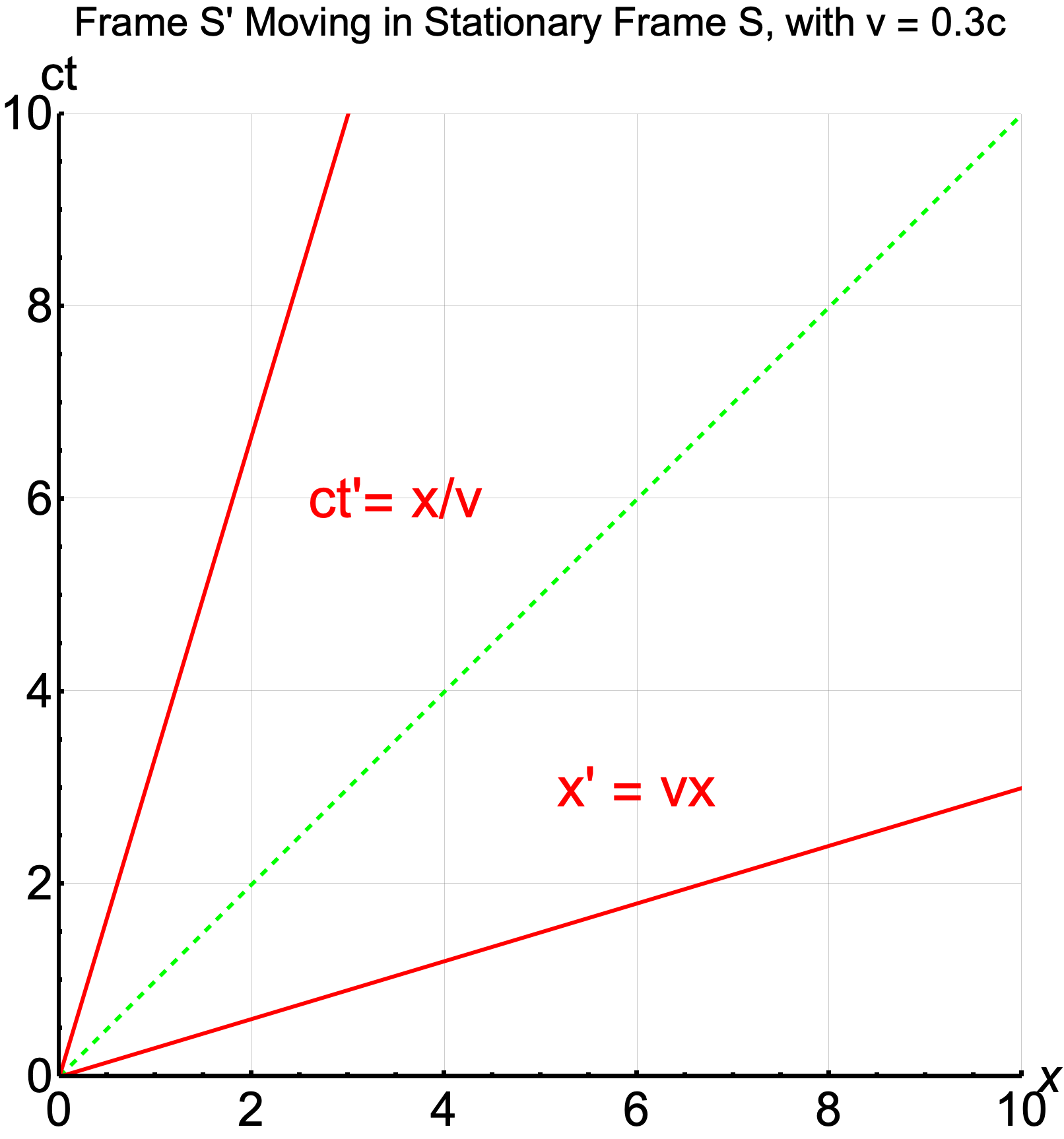
- The real value of Spacetime Diagrams is depicting the same event in inertial reference frames in relative motion.
- Using the Lorentz Transformations, we can draw, within a spacetime diagram for frame S, the ct′ and x′ axes for frame S′ moving with velocity v along the x-axis of S.
- The ct′ axis is x/v, in this case x/0.3.
- The x′ axis is xv, i.e. 0.3 x.
- View Derivation of Primed Axes from Lorentz Transformations
- The dotted green line represents a light ray, traveling at so many units of x per an equal number of units of ct.
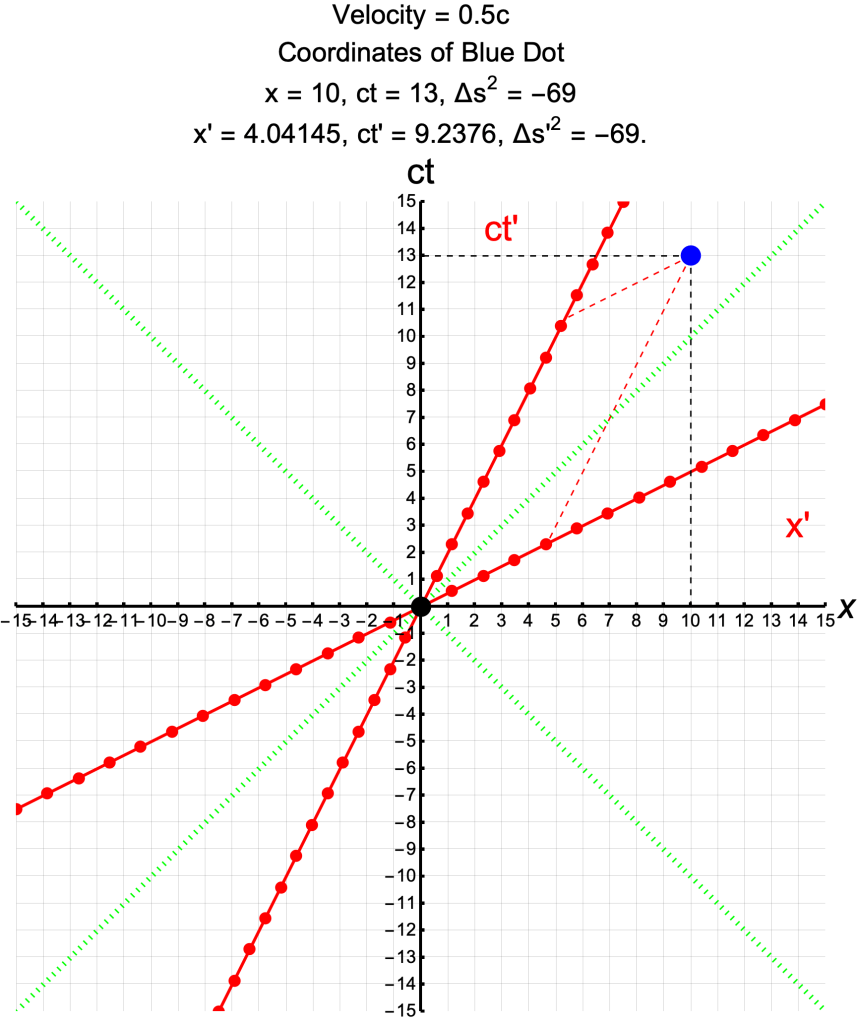
The Same Event in Different Frames
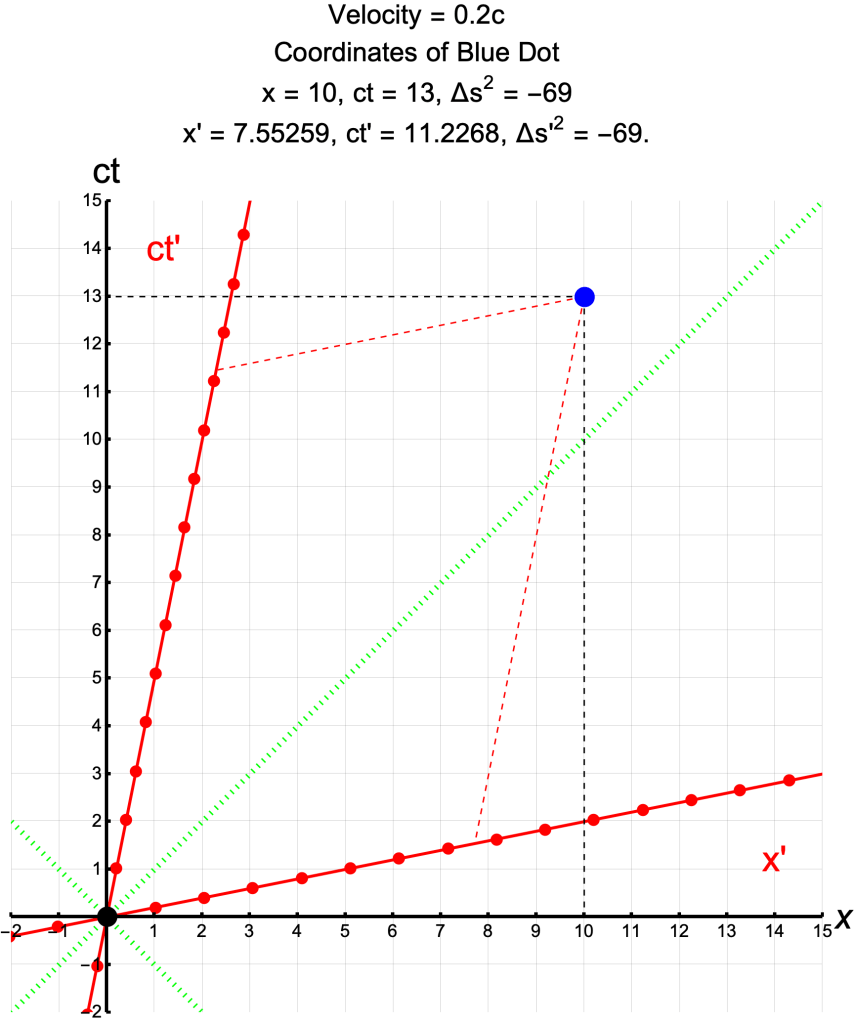
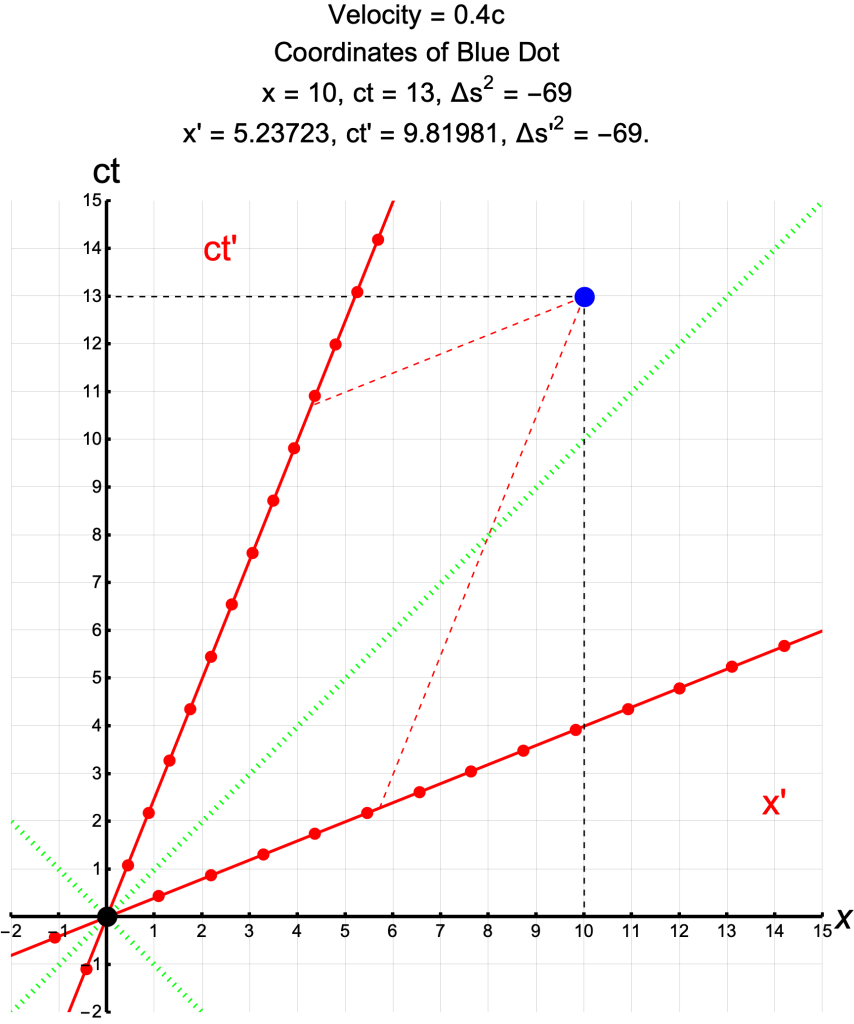
The Same Event in Frames at Different Velocities
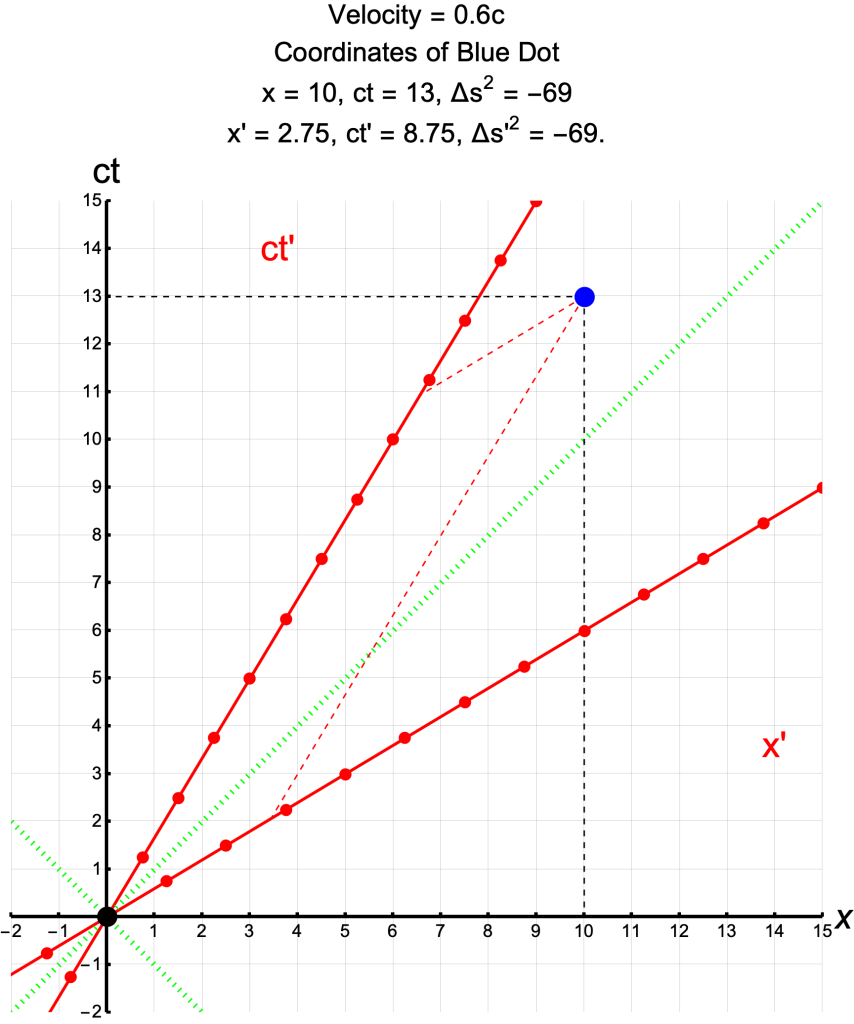
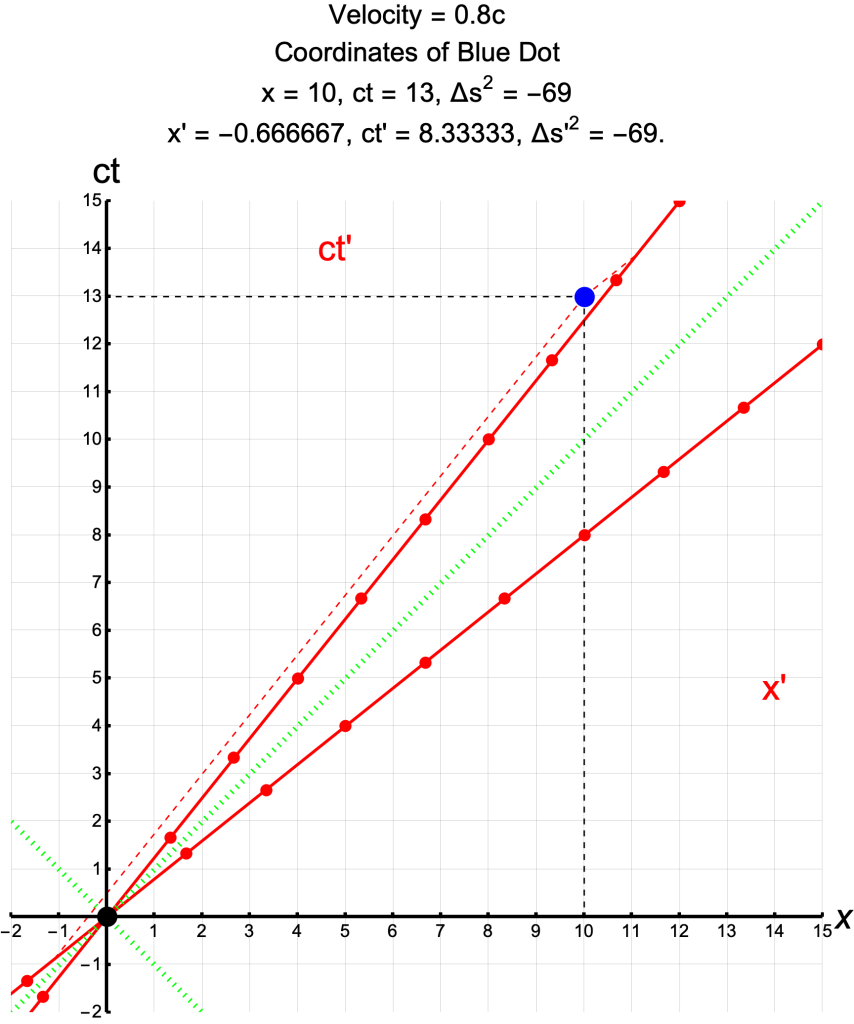
Applications
- Spacetime Diagram of Time Dilation
- Spacetime Diagram of Length Contraction
- Interactive Spacetime Diagrams
- Spacetime Diagram of Twin Paradox
- Spacetime Diagram of Speed of Light
- Spacetime Diagram of Timelike, Lightlike, and Spacelike intervals
- Hyperbola for Unit Spacetime Interval
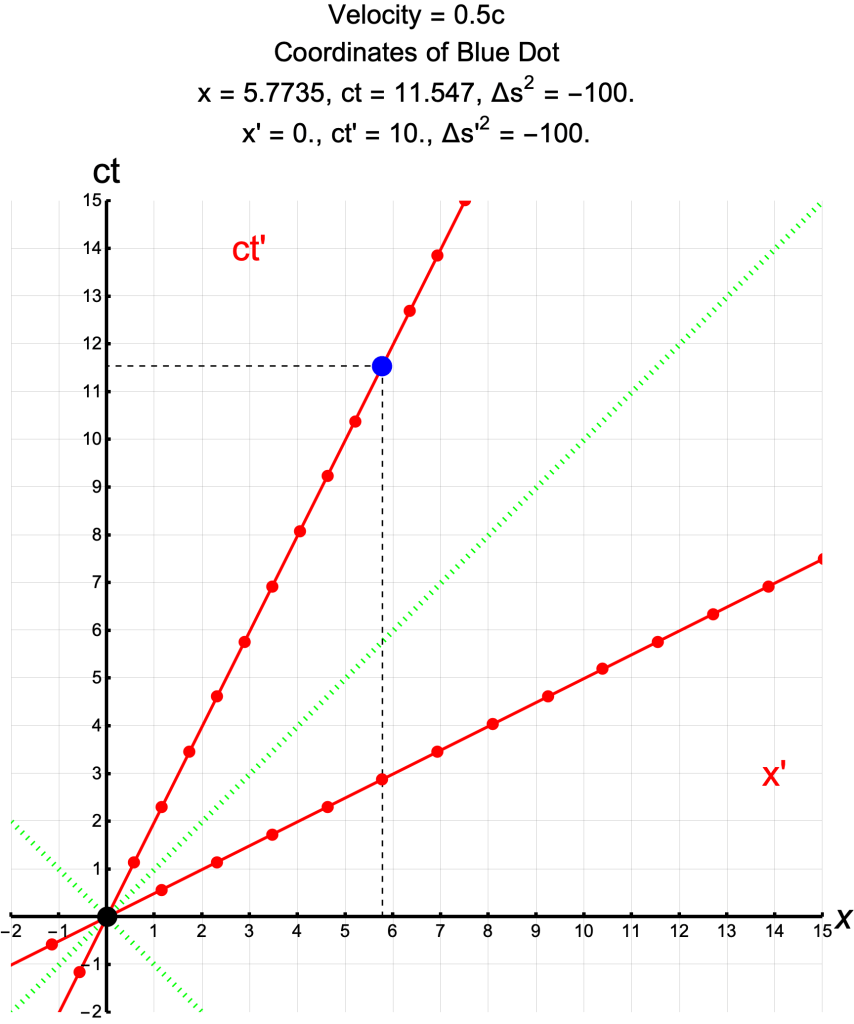
Spacetime Diagram of Time Dilation
- The interval between the black and blue events is 10 seconds in S′ (count the red dots) and 11.547 seconds in S.
- The events occur at the same location in S′ (at x′ = 0).
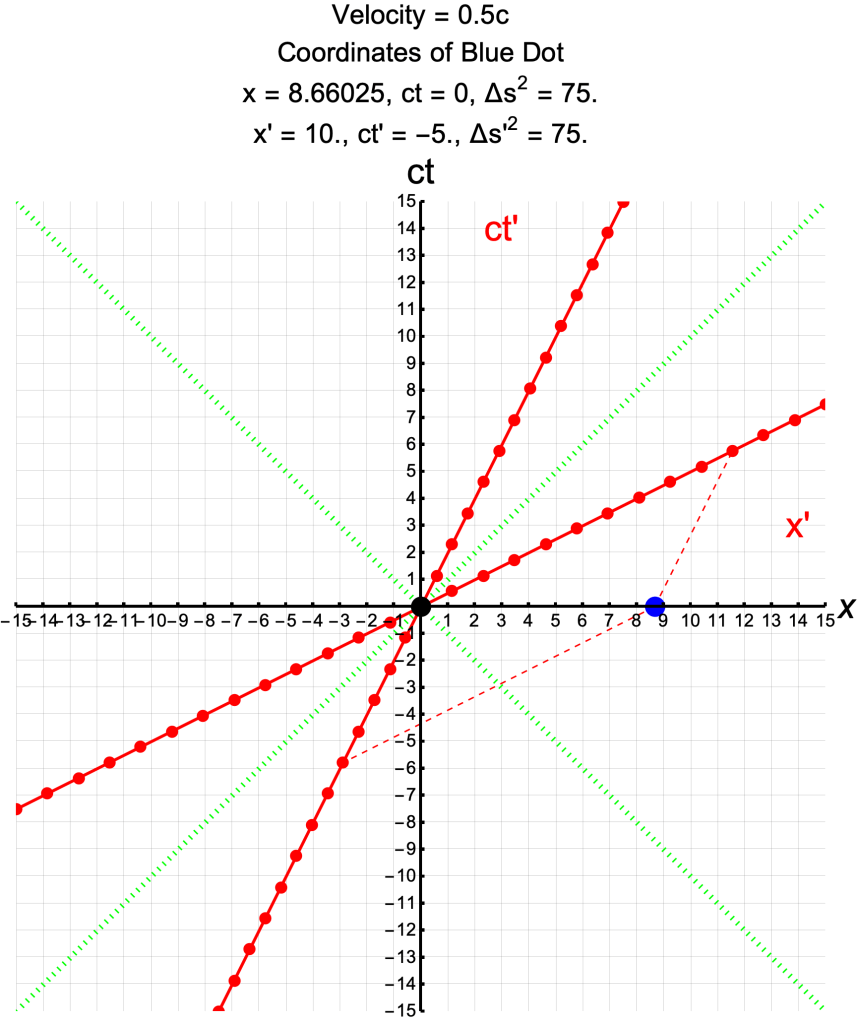
Spacetime Diagram of Length Contraction
- The blue and black events are the measurements of the ends of a rod.
- The distance between the measurements is 10 meters in S′ (count the red dots) and 8.66 meters in S.
- The measurements are simultaneous in S (at ct = 0).
Interactive Spacetime Diagrams
Spacetime Diagram of Twin Paradox

- In the Earth’s reference frame:
- The blue worldline represents the twin who stays on Earth for 10 years.
- The red worldline represents the twin who travels away from Earth for 5 years, turns around, and returns.
- The elapsed proper time of the stay-at home twin is 10 years:
- v = 0
- Proper time = coordinate time divided by 1/√(1 – (v/c)2) = 10 / 1 = 10 years.
- The elapsed proper time of the traveling twin is 6 years:
- v = 0.8 c
- Proper time = coordinate time divided by 1/√(1 – (v/c)2) = 10 / (5/3) = 6 years.
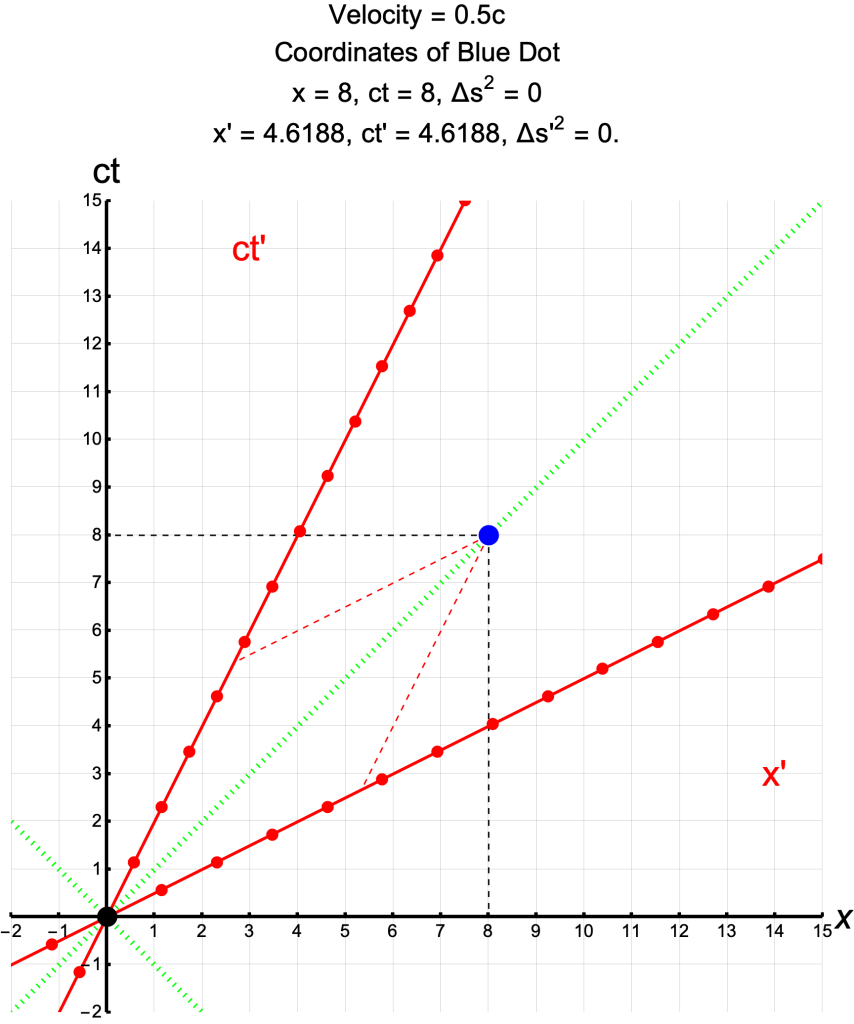
Spacetime Diagram of Speed of Light
- The blue dot is a photon.
- For the photon in frame S x/ct = 8/8 = 1
- which implies that x/t = c
- For the photon in frame S′, x′/ct′ = 4.6188/4.6188 = 1
- which implies that x′/t′ = c
- Not surprisingly, then, the speed of light = c in both frames S and S′.
Spacetime Diagram of Timelike, Lightlike, and Spacelike intervals
- A spacetime interval is timelike if Δs2 < 0, lightlike if Δs2 = 0, and spacelike if Δs2 > 0.
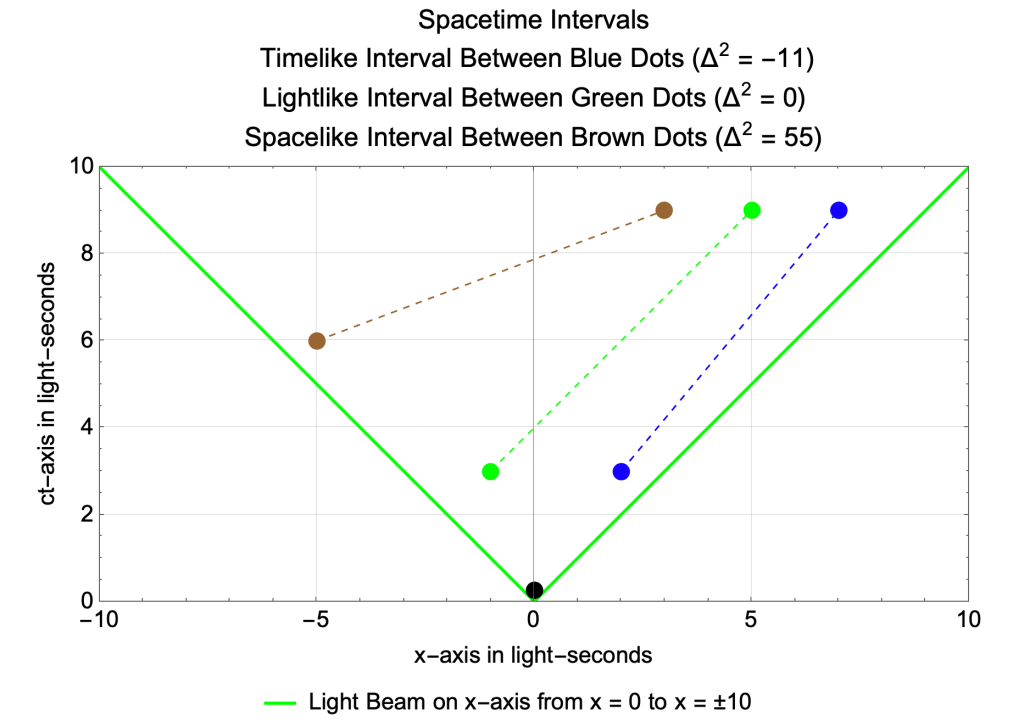
- The spacetime interval between the green events is lightlike.
- The dashed worldline between the green events is parallel to the green light beam, making a 45 degree angle with the x-axis. A particle traveling along the worldline moves at the speed of light and the interval is therefore lightlike.
- The spacetime interval between the blue events is timelike.
- The dashed worldline between the blue events makes an angle greater than 45 degrees with the x-axis. A particle traveling along the worldline moves at less than the speed of light and the interval is therefore timelike.
- The spacetime interval between the brown events is spacelike.
- The dashed worldline between the brown events makes an angle less than 45 degrees with the x-axis, meaning a particle would have to travel faster than light to make it from one to the other.
Hyperbola for Unit Spacetime Interval
- The spacetime interval (squared) is invariant across reference frames under the Lorentz Transformations:
- For any inertial frames S and S′, where S′ moves along the x-axis of S and ignoring y and z:
- –(ct)2 + x2 = –(ct′)2 + x′2
- For any inertial frames S and S′, where S′ moves along the x-axis of S and ignoring y and z:
- The formulas for the spacetime intervals of -1 and +1 are equations of hyperbolas:
- –(ct)2 + x2 = –1
- –(ct)2 + x2 = +1
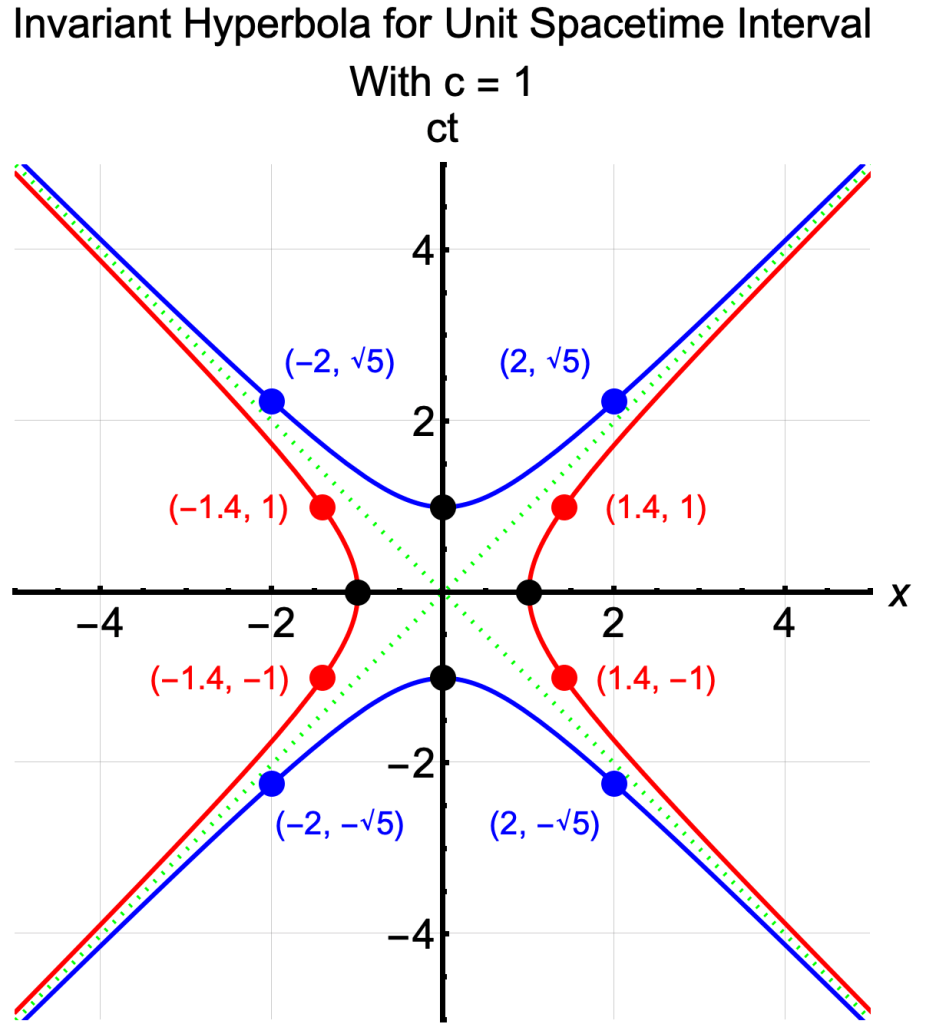
- The (timelike) points on the blue line satisfy the equation
- –(ct)2 + x2 = –1
- For example, for the four blue dots:
- –(√5)2 + 22 = –1
- –(√5)2 + (–2)2 = –1
- –(–√5)2 + (–2)2 = –1
- –(–√5)2 + 22 = –1
- The (spacelike) points on the red line satisfy the equation
- –(ct)2 + x2 = +1
- For example, for the four red dots:
- –(1)2 + (√2)2 = 1
- –(–1)2 + (√2)2 = 1
- –(–1)2 + (–√2)2 = 1
- –(1)2 + (–√2)2 = 1
- Finally, the four black dots represent the minima for ct and x:
- –(1)2 + (0)2 = –1 (proper time = 1)
- –(0)2 + (1)2 = 1
- –(-1)2 + (0)2 = –1 (proper time = 1)
- –(0)2 + (–1)2 = 1
Addendum
- Derivation of the Primed Axes of Spacetime Diagrams from Lorentz Transformations
- Proof of the Invariance of the Spacetime Interval from Lorentz Transformations
- Derivation of Time Dilation from Line Element
- Principles of Space and Time of Newtonian Mechanics
- Principles of Minkowski Spacetime
Derivation of the Primed Axes of Spacetime Diagrams from Lorentz Transformations
- Let S′ be a reference frame that moves along the x-axis of frame S at velocity v. The objective is to plot the x′ and ct′ axes of S′ within a Spacetime Diagram for S.
- x′ axis
- The equation for the x′ axis in the S′ frame is t′ = 0.
- The Lorentz Transformation for t′ is t′ = γ (t – v x/c2).
- Together, these propositions imply t = v x.
- Solve[Eliminate[{tp == γ (t – ((v x)/c2)), tp == 0}, tp], t]
- t = vx/c2
- Hence ct = v x
- Since c = 1 light-second / per second
- Solve[Eliminate[{tp == γ (t – ((v x)/c2)), tp == 0}, tp], t]
- ct′ axis
- The equation for the t′ axis in the S′ frame is x′ = 0.
- The Lorentz Transformation for x′ is x′ = γ(x – v t).
- Together, these propositions imply t = x / v.
- Solve[Eliminate[{xp = γ(x-v t) , xp = 0}, xp],t]
- t = x / v
- Solve[Eliminate[{xp = γ(x-v t) , xp = 0}, xp],t]
- Hence ct = x / v
- Since c = 1 light-second / per second
- x′ axis
Proof of the Invariance of the Spacetime Interval from Lorentz Transformations
- Spacetime interval:
- -(c Δt)2 + Δx2 + Δy2 + Δz2
- Derivation of invariance in Mathematica:
- Simplify[-c^2Δt^2 + Δx^2 + Δy^2 + Δz^2 == -c^2Δtp^2 + Δxp^2 + Δyp^2 + Δzp^2 /.
- {Δxp →(Δx – Δt v) / Sqrt[1 – v^2/c^2],
- Δtp → (Δt – (v Δx)/c^2) / Sqrt[1 – v^2/c^2],
- Δyp → Δy,
- Δzp → Δz} ]
- = True
Derivation of Time Dilation from Line Element
- 1. dτ2 = -(ds2)/c2
- Definition of proper time
- 2. dτ2 = -((-c2 dt2 + dx2 + dy2 + dz2)/c2)
- Replace ds2 in line 1 with line element
- Mathematica
- dτ^2 == -(ds^2)/c^2 /. ds^2 -> -(c^2 dt^2) + dx^2 + dy^2 + dz^2
- 3. dτ2 = (c2 dt2 – dx2 – dy2 – dz2)/c2
- Distribute negation sign in line 2
- 4. dτ2 = dt2 (1 – dx2/(c2 dt2) – dy2/(c2 dt2) – dz2/(c2 dt2))
- Multiply right side of 3 with dt2/dt2
- Mathematica
- dτ^2 == dt^2 Expand[(1/dt^2) ((c^2 dt^2 – dx^2 – dy^2 – dz^2)/c^2)]
- 5. dτ2 = dt2 (1 – (1/c2) ( dx2/dt2 + dy2/dt2 + dz2/dt2))
- Factor out 1/c2 in line 4
- Mathematica
- Simplify[1 – dx^2/(c^2 dt^2) – dy^2/(c^2 dt^2) – dz^2/(c^2 dt^2) == 1 – (1/c^2) ( dx^2/dt^2 + dy^2/dt^2 + dz^2/dt^2)]
- = True
- Simplify[1 – dx^2/(c^2 dt^2) – dy^2/(c^2 dt^2) – dz^2/(c^2 dt^2) == 1 – (1/c^2) ( dx^2/dt^2 + dy^2/dt^2 + dz^2/dt^2)]
- 6. dτ2 = dt2 (1 – (1/c2) (v2))
- Replace dx2/dt2 + dy2/dt2 + dz2/dt2 in line 5 with v2
- 7. dτ = Sqrt[dt2 (1 – (1/c2) (v2))]
- Take square root of both sides of line 6
- 8. dτ = dt Sqrt[(1 – v2/c2)]
- Pull dt2 out from under the radical sign in line 7
Principles of Space and Time of Newtonian Mechanics
- Space has three Cartesian coordinates, x, y, and z. Time has one coordinate, t.
- Time is absolute, i.e. intervals of time are the same in all inertial reference frames.
- Space is absolute, i.e. distances are the same in all inertial reference frames.
- Space is Euclidean, i.e. the line element of space, in Cartesian coordinates, is ds2 = dx2 + dy2 + dz2
- Galilean Transformations:
- For any inertial reference frames S and S′, whose origins and spatial axes coincide at t = t′ = 0 and where the origin of S′ moves along the x-axis of S in the positive x direction at velocity v:
- t′ = t
- x′ = x – vt
- y′ = y
- z′ = z
- For any inertial reference frames S and S′, whose origins and spatial axes coincide at t = t′ = 0 and where the origin of S′ moves along the x-axis of S in the positive x direction at velocity v:
Principles of Minkowski Spacetime
- Spacetime has four Cartesian coordinates, ct, x, y, and z, where
- t is in units of time
- c is the speed of light
- ct is in units of length
- (meters / second) x seconds = meters.
- Spacetime is absolute, i.e. intervals of spacetime are the same in all inertial reference frames.
- The spacetime is interval is Δs2 = -(c Δt)2 + Δx2 + Δy2 + Δz2.
- Distances and intervals of time are not the same in all inertial frames.
- Spacetime is hyperbolic, not Euclidean, i.e. the line element of spacetime, in Cartesian coordinates, is ds2 = -(c dt)2 + dx2 + dy2 + dz2.
- -t2 + x2 = a is an equation for a hyperbola.
- Lorentz Transformations:
- For any inertial reference frames S and S′, whose origins and spatial axes coincide at t = t′ = 0 and where the origin of S′ moves along the x-axis of S in the positive x direction at velocity v:
- t′ = γ(t – vx/c2)
- x′ = γ(x – vt)
- y′ = y
- z′ = z
- where γ is the Lorentz Factor:
- γ = 1/√(1 – v2/c2).
- For any inertial reference frames S and S′, whose origins and spatial axes coincide at t = t′ = 0 and where the origin of S′ moves along the x-axis of S in the positive x direction at velocity v: