Back to Special Relativity
Contents
- Principle of Relativity of Simultaneity
- Einstein’s Thought Experiment
- Derivation of the Relativity of Simultaneity from the Lorentz Transformations
Principle of Relativity of Simultaneity
- The Principle
- If two events are simultaneous in an inertial frame S (and are also physically separated along a given axis), the events are not simultaneous in an inertial frame in motion relative to S (along the axis).
- The principle follows from Einstein’s postulate that the speed of light equals c in every inertial reference frame.
- It can also be derived from the Lorentz Transformations.
Einstein’s Thought Experiment
- It’s important to bear in mind that the Constancy of the Speed of Light implies not only that the speed of light is the same in every inertial frame but also that it’s finite. So stuff can happen while light is in transit.
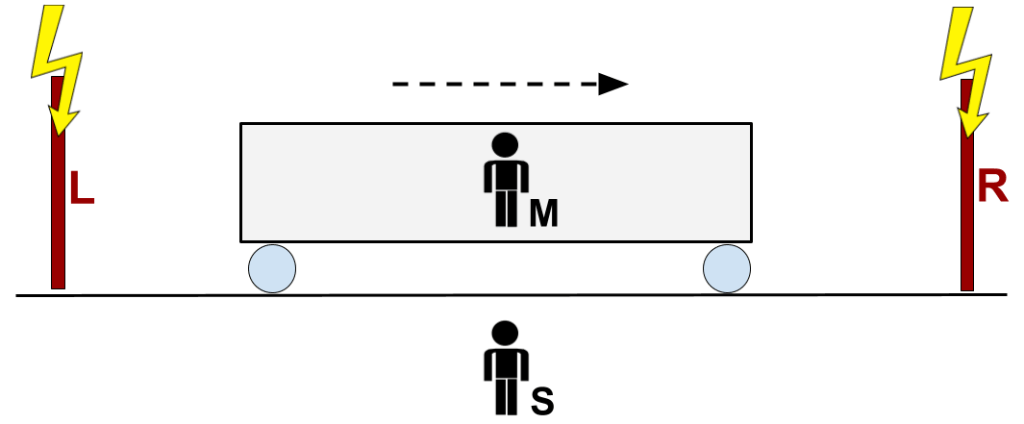
- Observer S watches a high-speed train pass by left to right as lightning strikes telephone poles R and L.
- S, who’s equidistant from L and R, sees lightning hit the poles at the same time. Since light travels at the same speed, c, the lightning strikes are simultaneous in S‘s reference frame.
- A passenger on the train, M, also sees the lightning strikes. But M is moving toward R and away from L while the light rays are in transit. (The speed of light is finite.) He therefore sees lightning strike R before it strikes L. The lightning strikes are therefore consecutive in M‘s reference frame, not simultaneous.
View Animation of Light Rays in the S and M Frames
Calculation using Lorentz Transformation
- Assume that in S‘s frame the lightning strike at location L occurs at
- location xL = -60,000 meters
- time tL = 1.0 seconds
- And the strike at R occurs at
- location xR = 60,000 meters
- time tR = 1.0 seconds
- The lightning strikes are thus simultaneous in S‘s frame.
- Suppose that M‘s velocity is 4/5 the speed of light relative to S. Then, using the Lorentz Transformation for time, lightning hits poles L and R in M‘s frame at
- t′L = 1.6669 seconds
- t′R = 1.6664 seconds
- The math:
- t′ = (t – vx/c2)/√(1 – v2/c2)
- c = 300,000,000 m/s
- v = 0.8 c
- t = 1.0 seconds
- xL = -60,000 meters
- t′L = 1.6669 seconds
- xR = 60,000 meters
- t′R = 1.6664 seconds
- So in M‘s frame the lightning strike at R occurs a fraction of a second before the strike at L.
Derivation of the Relativity of Simultaneity from the Lorentz Transformations
- 1. Δt′ = γ(Δt – vΔx/c2)
- where γ = 1 /√ (1 – v2/c2)
- Lorentz Transformation for time
- 2. Δt = 0
- Events are simultaneous in the unprimed frame
- 3. Δt′ = -(γvΔx)/c2)
- From 1 and 2
- 4. (γvΔx)/c2) > 0
- Δx > 0 because events are spatially separated in the unprimed frame
- v > 0 because frames are in relative motion
- γ > 0
- c2> 0
- 5. Δt′ ≠ 0
- From 3 and 4