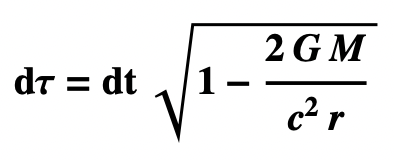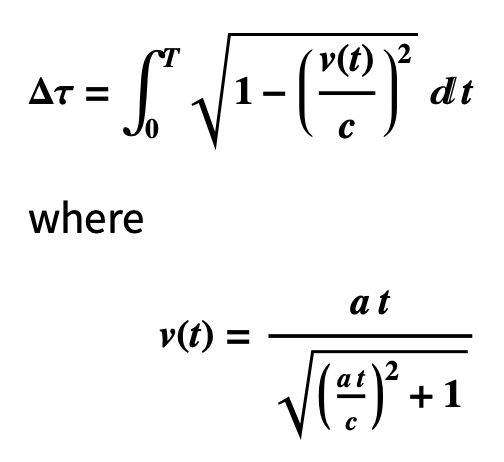Twin Paradox

Back to Special Relativity

Contents

The Paradox

Time Dilation applies not only to clocks, spaceships, and subatomic particles; it also applies to living organisms.
The Twin Paradox, which derives from a 1911 thought-experiment by French physicist Paul Langevin, raises three questions:
- Why does the traveling twin age less and not the twin who remains on Earth?
- Can Special Relativity resolve the paradox? Or is General Relativity required?
- To what degree does the Earthbound twin age less due to gravitational time dilation?

Alice and Bob

Alice and Bob are twins. When they’re 20 years old, Alice travels by spaceship to Barnard’s Star and back while Bob remains on Earth. Alice’s spaceship travels at a constant speed of 80 percent of the speed of light (apart from a week or so accelerating and decelerating). Barnard’s Star is six light years from Earth. So, Alice is gone for 15 years (in Bob’s reference frame).
- 12 light years / 0.8 light years per year = 15 years.
When she returns, Alice is 29 years old and Bob is 35.
- Alice’s elapsed time = Δτ = √[1 – v²/c²] Δt = √[1 – 0.8²] x 15 = 9 years.

The Questions

Motion is relative: if an object moves relative to a second, the second moves relative to the first. Since Alice’s spacecraft moves relative to Earth, the Earth moves relative to her spacecraft. So why is Alice younger than Bob rather than Bob younger than Alice?
Einstein’s postulates are about inertial reference frames. But Alice’s frame is not inertial since it undergoes acceleration. It thus seems that Special Relativity can’t resolve the paradox and recourse must be made to General Relativity.
There are two sources of time dilation: relative motion (per Special Relativity) and gravity (per General Relativity). The twin paradox concerns the former. But Bob is within Earth’s gravitational field for 15 years and is thus subject to gravitational time dilation. How, then, does the amount of time Bob ages less than Alice because of gravity compare to the amount of time Alice ages less than Bob because of relative motion?

Why is Alice younger than Bob rather than Bob younger than Alice?

Physicists give two reasons for the asymmetry between Alice and Bob.
- Alice’s frame accelerates and Bob’s doesn’t.
- Alice’s worldline comprises two inertial reference frames while Bob’s has only one.
The question can be put this way:
- Is acceleration an essential part of the reason why Alice is younger than Bob? Or is acceleration required only so that Alice’s worldline is split into two inertial frames?
Two variants of the twin paradox suggest that acceleration per se plays no role.
- Outgoing and Incoming Inertial Spaceships
  - Suppose that Alice’s spaceship passes by Earth at 80 percent of light speed (when Alice is 20), passes by Barnard’s Star (when Alice is 24 ½), and keeps going.
  - As Alice’s spaceship travels away from Earth, a second spaceship, with Carol on board, travels toward Earth at 80 percent of the speed of light. It passes by Alice’s spaceship just as they both pass Barnard’s Star (when Alice and Carol are both 24 ½), passes by Earth (when Carol is 29), and keeps going.
  - Alice and Carol’s frames are both inertial. And, between them, they age 9 years compared to Bob’s 15.
- Alice’s Inertial Frames While Coasting
  - Suppose Alice signals Bob whenever she stops accelerating and whenever she starts decelerating. The frames between signals — outgoing and incoming — are inertial and therefore within the scope of Einstein’s postulates, the Lorentz Transformations, and Time Dilation.

Can Special Relativity resolve the paradox?

Arguments SR can’t resolve the paradox:
- Einstein’s postulates apply only to inertial reference frames. Alice’s frame is not inertial. Therefore Special Relativity doesn’t apply to Alice’s frame.
- The Lorentz transformations, from which Time Dilation is derived, apply only to frames moving relative to each other at a constant velocity. But the velocity between the twin’s frames isn’t constant when Alice’s spaceship is accelerating.
Arguments SR can resolve the paradox:
- James Hartle’s Argument by Analogy:
  - Newton’s Laws are valid only in inertial frames. Yet you can calculate the acceleration of an object even though the reference frame in which the object is at rest is not inertial. Einstein’s postulates are likewise valid only in inertial frames. Yet you can calculate the proper time of a spaceship whose frame is accelerating.
- Minkowski Flat Spacetime
  - In 1908 Herman Minkowski extended Einstein’s Special Relativity to flat spacetime, i.e. spacetime without gravity. Alice travels through spacetime that’s (virtually) flat. Therefore, Minkowski’s extension of Special Relativity (in particular his concept of proper time) applies to Alice’s trip to Barnard’s Star.
  - (The slight spacetime curvature caused by Earth and St Bernard’s Star can be eliminated by moving Alice and Bob to spaceships in intergalactic space.)

Quotes on Resolving the Paradox

Special Relativity Cannot Resolve the Paradox
- Sidney Perkowitz, britannica.com/science/twin-paradox
  - “The situation is not appropriately treated by special relativity. To return to Earth the spacecraft must change direction, which violates the condition of steady straight-line motion central to special relativity. A full treatment requires general relativity, which shows that there would be an asymmetrical change in time between the two twins.”
- Dept of Astronomy at Georgia State, hyperphysics.phyastr.gsu.edu/hbase/Relativ/twin.html#c1
  - “The scenario is complicated by the fact that the traveling twin must be accelerated up to traveling speed, turned around, and decelerated again upon return to Earth. Accelerations are outside the realm of special relativity and require general relativity.”
- Valerio Faraoni, Special Relativity, 2013, Footnote page 23
  - “Locally, acceleration is equivalent to a gravitational field and is properly treated in General Relativity.”

Special Relativity Can Resolve the Paradox
- James Hartle, Gravity: An Introduction to Einstein’s General Relativity, 2003, page 62, footnote 9
  - “It’s a misconception that special relativity can deal only with motion at constant velocity. Nothing could be further from the truth. This mistaken idea possibly stems from the fact that inertial frames can differ by uniform motion but not accelerated motion. But this is equally true in Newtonian mechanics, which is mainly concerned with explaining accelerated motion.”
- Sean Carroll, Spacetime and Geometry: an Introduction to General Relativity, 2004
  - “In particular there is no truth to the rumor that Special Relativity is unable to deal with accelerated trajectories, and general relativity must be invoked. General Relativity becomes relevant in the presence of gravity, when spacetime is curved. Any processes in flat spacetime are described within the context of Special Relativity.”

How much less does Bob age because of gravity?

Alice is younger than Bob by 6 years because of their relative motion. By contrast, due to Earth’s gravitational field, Bob is younger than Alice by ⅓ of a second.

How Bob Loses 1/3 of a second
- Formula for Gravitational Time Dilation
- where
  - dτ = proper time at the Earth’s surface
  - dt = coordinate time in intergalactic space
  - G = gravitational constant
    - 6.67384 10^-11
  - M = mass of Earth
    - 5.972 * 10²⁴ kg
  - r = radius of Earth
    - 6.37101 * 10⁶ meters
  - c = speed of light
    - 2.99792458 * 10⁸ m/s
- Milliseconds Bob loses in a year (in Mathematica)
  - factor = Sqrt[1 – (2 G m)/(r c^2)]
  - secondsinyear = 31536000
  - (secondsinyear – factor secondsinyear) 1000
  - 21.95 milliseconds
- Time Bob loses in 15 years
  - 21.95 * 15 = 329.25 milliseconds ≈ ⅓ of a second

Calculation of Alice’s Elapsed Time in Minkowski Spacetime

Formulas:
- Line element of flat spacetime: ds² = −(c dt)² + dx² + dy² + dz²
- Definition of proper time element: dτ² = −ds²/c²
- Formula for dτ in terms of dt: dτ = √[1 – v²/c²] dt
Bob’s Worldline
- Spacetime distance (in light years squared with c = 1 light year per year)
  - Δs² = -(15 c)² + 0² = -(15 c)²
- Proper time (in years)
  - Δτ² = −ds²/c² = 15²
  - Δτ = 15
Alice’s Wordline
- Without Acceleration
  - Proper time (in years)
    - Δτ = √[1 – v²/c²] Δt = √[1 – 0.8²] 15 = 9 years
  - See Spacetime Diagram
- With Acceleration
  - Assume that Alice’s spaceship accelerates at 2,315 meters-per-second per second attaining a velocity of 80 percent of light speed in two days in Bob’s frame. That’s 1.65 days in Alice’s frame. (See Acceleration Calculation.)
  - Alice’s trip has two periods of acceleration, coming and going, and two periods of deceleration. That’s 1.65 x 4 = 6.6 days in Alice’s frame.
  - So Alice’s total elapsed time with acceleration is 9 years + 6.6 days.

Acceleration Calculation
- Formula for Alice’s elapsed proper time Δτ for a period of T seconds at acceleration = a in Bob’s frame (Wikipedia):
Calculation in Mathematica
- (* Formulas *)
  - v[t_] := (at)/Sqrt[((at)/c)^2 + 1]
  - Δτ = FullSimplify[Integrate[Sqrt[1 – (v[t]/c)^2], {t, 0, T}], Assumptions -> {Reals, c > 0, a > 0, t > 0, T > 0}]
- (* Output of Integration *)
  - Δτ = (c ArcSinh[(a T)/c]) / a
- (* Replace c with speed of light, a with acceleration 2315, T with 2 days of seconds *)
- (* Then divide by 1 day of seconds *)
  - N[(c ArcSinh[(a T)/c])/ a /. {c → (3 10^8), a → 2315, T → 172800}] / 86400
- (* We get Alice’s proper time in days *)
  - 1.64788
- (* Alice’s velocity in Bob’s frame after two days of acceleration at 2315 m/s² *)
  - N[(a t)/Sqrt[1 + ((a t)/c)^2] /. {a → 2315, c → 3 10^8, t → 172800}]
- (* Output equals 80 percent of speed of light *)
  - 2.40007*10^8

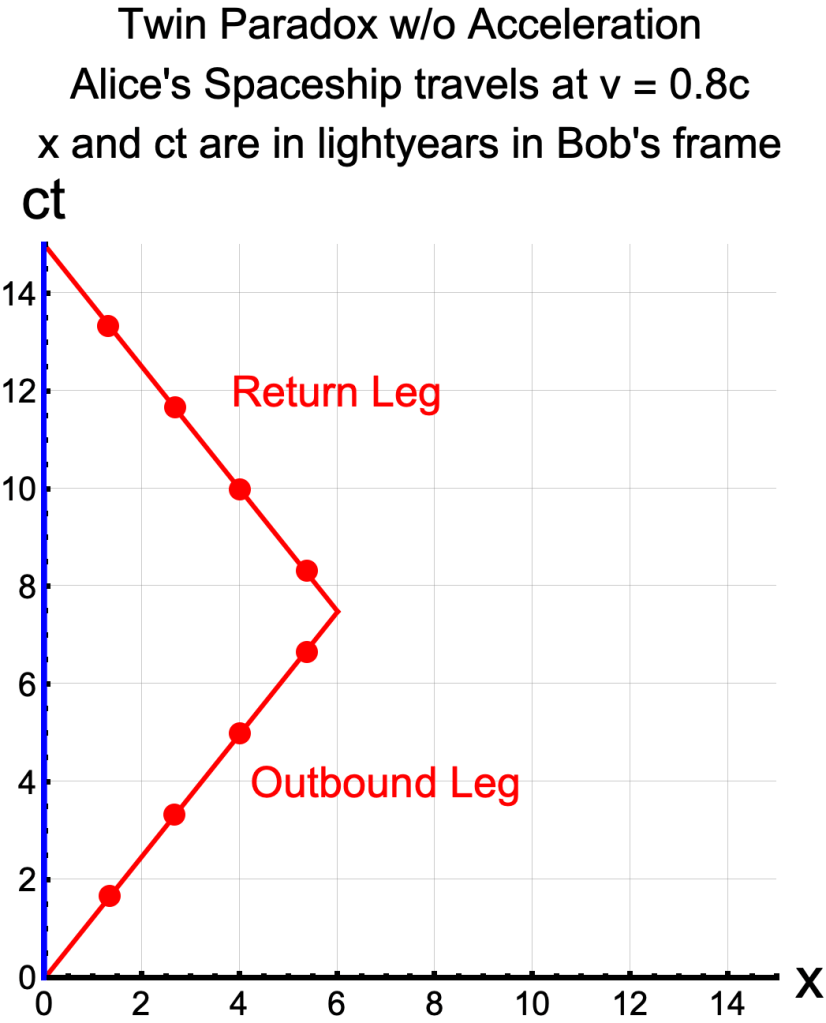
Spacetime Diagram for Twin Paradox

Alice travels to the right on the x-axis for a distance of 6 lightyears in Bob’s frame.
At the 7.5 year mark on the ct-axis (in Bob’s Frame) she turns around and heads back to Earth.