Outline
- Bayes Theorem
- Comparative Form of Bayes Theorem
- Three Ways to Calculate Probabilities Using Bayes Theorem
- Green Cabs and Blue Taxis
- Probability You’re Sick if You Test Positive
- Probability You’re Not Sick if You Test Negative
- Comparative Forms of Bayes Theorem
- Non-Comparative Form of Bayes Theorem
- Derivation of Bayes Theorem
Bayes’ Theorem
- Bayes’ Theorem formalizes the idea that the probability of a hypothesis given the evidence is, in part, a function of the probability of the evidence given the hypothesis.
- The simplest example of Bayes’ Theorem:
- Two coins are on a table, both heads up. One is a regular coin, the other is double-headed. You don’t know which is which. You randomly select one of the coins and, without looking, flip it. It lands heads.
- Before flipping, the probability you selected the double-headed coin was 1/2.
- That the coin landed hands makes it more likely the coin you selected is double-headed. According to Bayes’ Theorem, the probability is 2/3.
- The mathematical calculation:
- P(D) = 0.5 and P(S) = 0.5, where
- D is the hypothesis that the coin you selected is the double-headed coin;
- S is the hypothesis that the coin you selected is the regular single-headed coin.
- P(E|D) = 1 and P(E|S) = 1/2
- where E (the evidence) is that the coin landed heads.
- Bayes’ Theorem
- P(D|E) = P(D) P(E|D) / ((P(D) P(E|D) + (P(S) P(E|S))
- Therefore P(D|E) = (1/2 * 1) /(1/2 * 1 + 1/2 * 1/2) = 0.5 /(0.5 + 0.25) = 2/3
- That is, the probability that you selected the double-sided coin, given the evidence, is 2/3.
- Which is to say that, after the coin landed heads, the probability of the double-headed hypothesis is higher because it better predicted the evidence.
- P(D) = 0.5 and P(S) = 0.5, where
- Main forms of Bayes’ Theorem:
- The Comparative Form formalizes the principle that a hypothesis that better predicts the evidence is more probable, other things being equal.
- The Non–comparative Form quantifies the idea that the more unexpected a prediction, the more likely the hypothesis, other things being equal.
Comparative Form of Bayes’ Theorem
- The Comparative Form of Bayes Theorem formalizes the principle that a hypothesis that better predicts the evidence is more probable, other things being equal.
- Specifically, it defines the numeric probability of a hypothesis in light of the evidence, based on:
- the probability of the evidence given competing hypotheses,
- the probability of competing hypotheses apart from the evidence.
- Comparative Form of Bayes Theorem for Two Hypothesis:

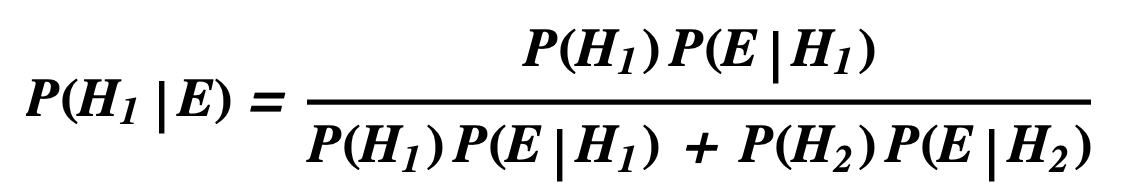
- H1 is the hypothesis under consideration
- H2 is a competing hypothesis
- Either H1 or H2 is true but not both
- E is the evidence
- P(- – -) means the probability that – – –
- P( – – – | …… ) means the probability that – – – given that …..
Three Ways to Calculate Probabilities Using Bayes’ Theorem
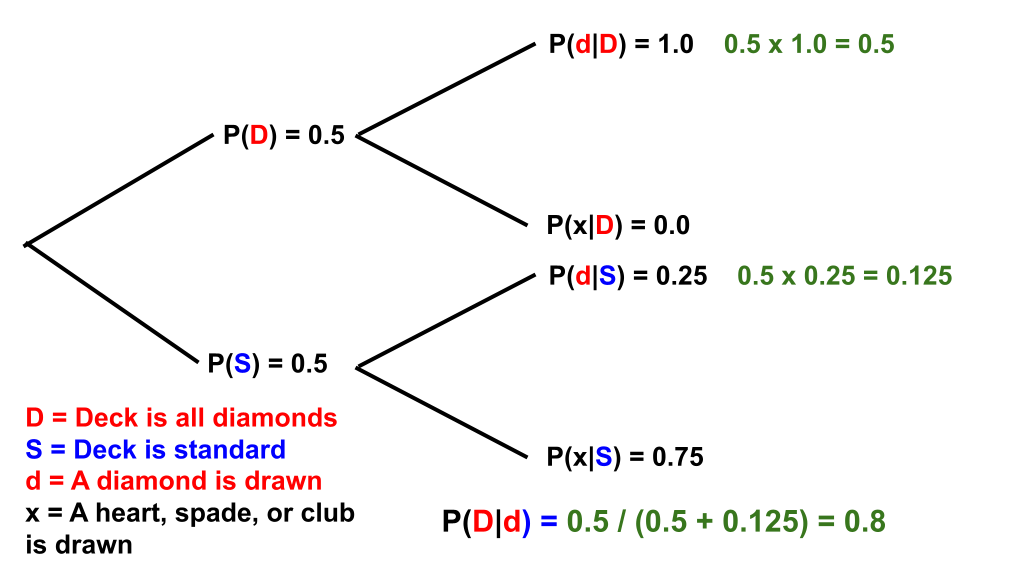
- There are two decks of cards on the table, face down.
- One is a standard deck of 52 cards
- The other consists of 52 diamonds: four aces of diamonds, four kings of diamonds, and so on.
- You randomly select one of the two decks, not knowing which. The probability you selected the deck of diamonds = 0.5.
- You randomly draw a card from the selected deck. The card is a diamond.
- According to Bayes Theorem, the fact that you drew a diamond makes it more likely that the selected deck is the deck of diamonds. In fact, per Bayes Theorem, the probability increased from 0.5 to 0.8.
- The 0.8 probability is calculated from Bayes Theorem using three pieces of information:
- Before you drew the diamond, the probability that you had selected the deck of diamonds = 0.5.
- The probability of drawing a diamond from the deck of diamonds = 1.0
- The probability of drawing a diamond from the standard deck of cards = 0.25
Using a Bayesian Calculator
- Abbreviations
- H1 = hypothesis the selected deck is a deck of 52 diamonds
- H2 = hypothesis the selected deck is a standard deck of 52 cards
- E = the evidence, i.e. that you drew a diamond from the selected deck
- Prior Probabilities, before you draw a card.
- Prior probability of H1 = P(H1) = 0.5
- Prior probability of H2 = P( H2) = 0.5.
- Likelihoods of E given the hypotheses
- Probability of E given H1 = P(E|H1) = 1.0
- Probability of E given H2 = P(E|H2) = 0.25
- Results: Posterior Probabilities
- Probability of H1 given E = P(H1|E) = 0.8
- Probability of H2 given E = P(H2|E) = 0.2

Using a Probability Tree
Using Bayes Formula

Green Cabs and Blue Taxis
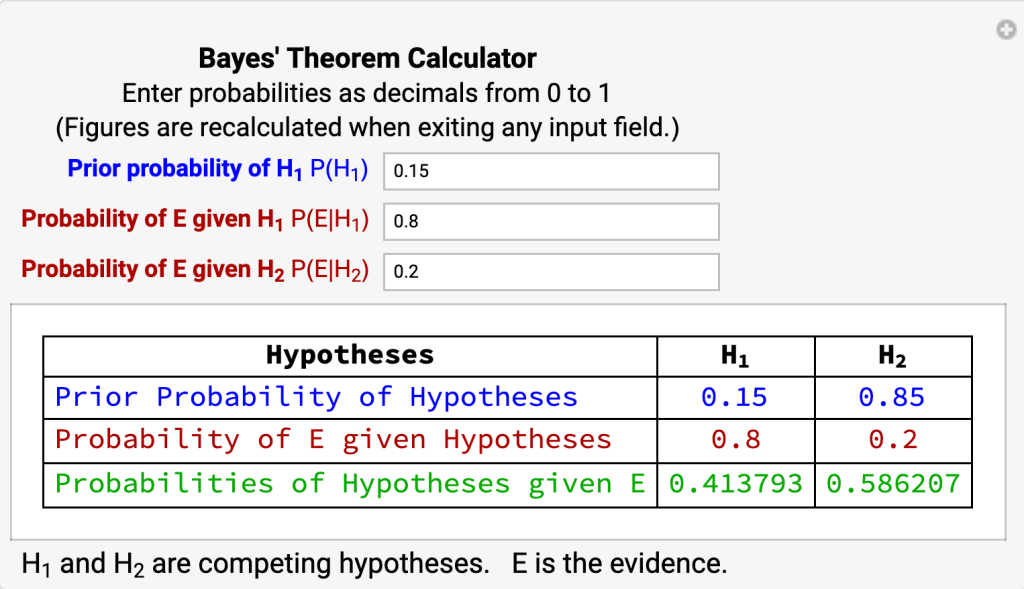
- 85 percent of taxis in a city are Green Cabs. The other 15 percent are Blue Taxis. A taxi sideswiped another car on a misty winter night and drove off. A witness testified the taxi was blue. The witness is tested under conditions like those on the night of the accident and she correctly identifies the color of the taxi 80% of the time. What’s the probability the sideswiper was a Blue Taxi?
Using a Bayesian Calculator
- H1 = the taxi is blue
- H2 = the taxi is green
- E = the witness testifies the taxi is blue.
Using a Probability Tree

Using Bayes Formula
- P(B|b) = P(b/B) x P(B) / ( P(b/B) x P(B) + P(b|G) x P(G) )
- B = the taxi is blue
- G = the taxi is green
- b = the witness testifies the taxi is blue.
- P(B) = 0.15
- P(b/B) = 0.8
- P(G) = 0.85
- P(b|G) = 0.2
- Therefore, P(B|b) = (0.8 x 0.15) / (0.8 x 0.15 + 0.2 x 0.85) = 0.41.
Probability You’re Sick if You Test Positive
View Sensitivity, Specificity, Positive and Negative Predictive Values
- Issue
- You test positive for a disease. What’s the probability you’re sick, i.e. P(sick | positive)?
- Given
- Sensitivity of the test = P(positive | sick) = 98.1%
- Specificity of the test = P(negative | not sick) = 99.6%.
- Prevalence of disease in the population = P(sick) = 5%
- Calculate
- P(sick | positive) = ?
- Abbreviations
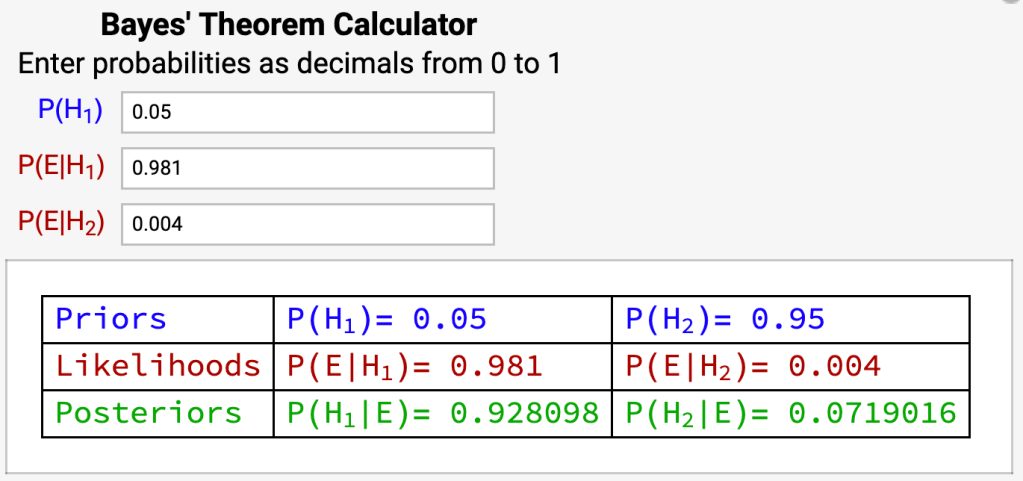
- H1 = You’re sick
- H2 = You’re not sick
- E = You test positive
- Prior Probabilities, based on prevalence:
- Prior probability of H1 = P(H1) = 0.05
- Prior probability of H2 = P( H2) = 0.95
- Likelihoods of E given the hypotheses
- Probability of E given H1 = P(E|H1) = 0.981
- based on the sensitivity of the test
- Probability of E given H2 = P(E|H2) = 1 – 0.996 = 0.004
- based on the specificity of the test
- Probability of E given H1 = P(E|H1) = 0.981
- Results: Posterior Probabilities
- Probability of H1 given E = P(H1|E) = 0.928
- Probability of H2 given E = P(H2|E) = 0.072
- So
- P(sick | positive) = P(H1|E) = 92.8%
Probability You’re Not Sick if You Test Negative
- Issue
- You test negative for a disease. What’s the probability you’re not sick, i.e. P( not sick | negative)?
- Given
- Sensitivity of the test = P(positive | sick) = 98.1%
- Specificity of the test = P(negative | not sick) = 99.6%.
- Prevalence of the disease in the population = P(sick) = 5%
- Calculate
- P(not sick | negative) = ?
- Abbreviations
- H1 = You’re sick
- H2 = You’re not sick
- E = You test negative
- Prior Probabilities, based on prevalence:
- Prior probability of H1 = P(H1) = 0.05
- Prior probability of H2 = P( H2) = 0.95
- Likelihoods of E given the hypotheses
- Probability of E given H1 = P(E|H1) = 1 – 0.981 = 0.019
- based on the sensitivity of the test
- Probability of E given H2 = P(E|H2) = 0.996
- based on the specificity of the test
- Probability of E given H1 = P(E|H1) = 1 – 0.981 = 0.019
- Results: Posterior Probabilities
- Probability of H1 given E = P(H1|E) = 0.001
- Probability of H2 given E = P(H2|E) = 0.999
- So
- P(not sick | negative) = P(H2|E) = 99.9%

View Random Drug Test
Comparative Forms of Bayes Theorem
Two Competing Hypotheses
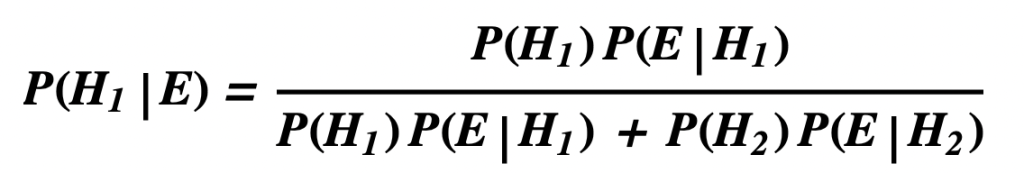
Single Hypothesis, True and False
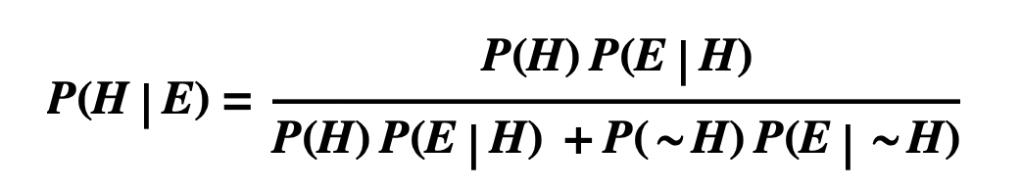
Number n of Competing Hypotheses
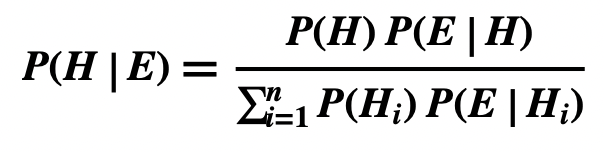
Hypotheses are Discrete Random Variables 𝞱
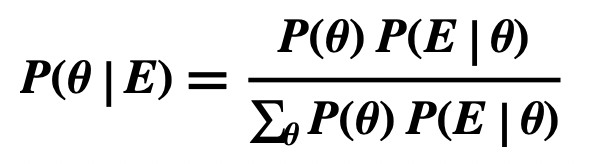
Hypotheses are Continuous Random Variables 𝞱
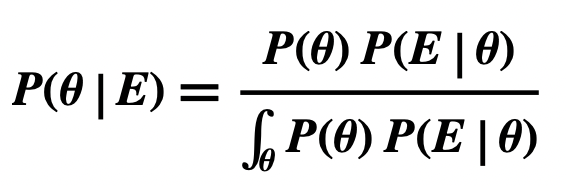
Non-Comparative Form of Bayes Theorem
- The Non-Comparative Form of Bayes Theorem quantifies the idea that the more unexpected a prediction, the more likely the hypothesis, other things being equal. That is, the lower P(E), the greater P(H | E).
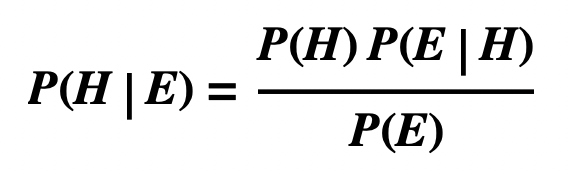
- H is the hypothesis under consideration
- E is the evidence
- P(- – -) means the probability that – – –
- P( – – – | …… ) means the probability that – – – given that …..
- View Bayesian Estimation for the application of the Non-comparative Form to statistical estimation.
Derivation of Bayes Theorem
Derivation of Comparative Form (Single Hypothesis)
- P(H|E) = P(H&E) / P(E)
- Definition of Conditional Probability
- P(H|E) = P(H&E) / P((E&H) v (E&~H))
- Equivalence Rule
- E is logically equivalent to E&H v E&~H
- P(H|E) = P(H&E) /( P(E&H) + P(E&~H) )
- Special Disjunction Rule
- P(H|E) = P(H) P(E|H) /( P(H) P(E|H) + P(~H) P(E|~H) )
- General Conjunction Rule
Derivation of Non-Comparative Form
- P(H|E) = P(H&E) / P(E)
- Definition of Conditional Probability
- P(H|E) = P(H) P(E|H) / P(E)
- General Conjunction Rule