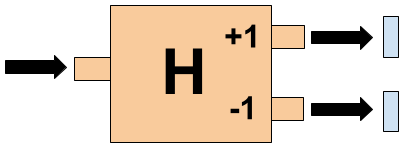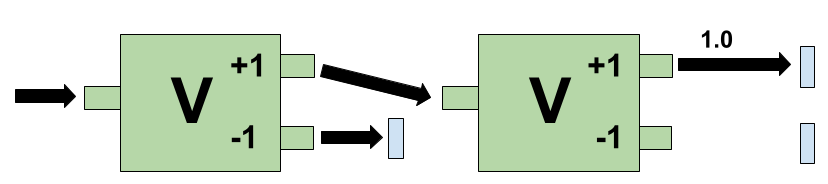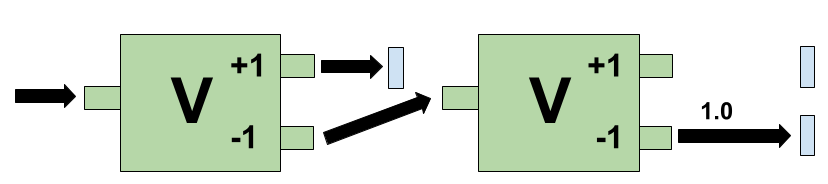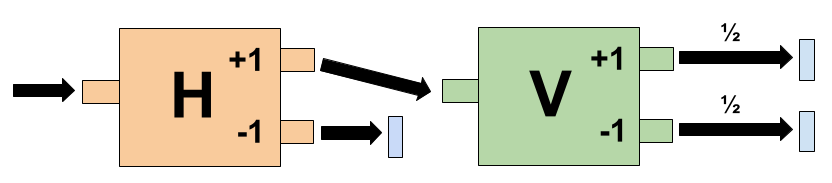Double Path Experiment

Back to Quantum Mechanics

Table of Contents

Introduction

Classical Mechanics predicts what happens in a physical system. But Quantum Mechanics predicts only the outcome of a measurement. So it’s natural to wonder what goes on in a quantum system between measurements. Widely discussed in this regard is the classic double-slit experiment. This page is devoted to a different example, just as puzzling: the double-path experiment.

Electron Spin

In addition to mass and electric charge an electron has intrinsic angular momentum called spin, which has one of two values relative to a defined axis: spin-up and spin-down. Spin and electric charge combine to make an electron into a tiny magnet. This means that an electron’s spin can be measured by a magnet that deflects a moving electron either north or south.
The two-path experiment uses two magnets to measure an electron’s spin: one measures spin along a vertical axis; the other that measures spin along a horizontal axis.

The Vertical Spin Magnet

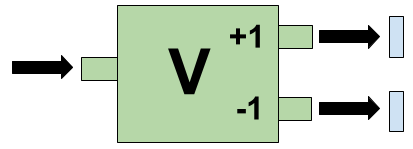
The vertical spin magnet measures the spin of an electron along the vertical axis:
An electron enters the port on the left and exits one of the two ports on the right. An electron exiting through the upper port hits the upper detecting screen, indicating its vertical spin = +1. An electron exiting the lower port hits the lower detecting screen, indicating its vertical spin = -1.
The vertical spin magnet is represented in Quantum Mechanics by an operator whose matrix form is:
- - (This is the Pauli matrix for σ_z.)
The operator’s eigenvectors and eigenvalues are:
- Eigenvector |{1, 0}> with eigenvalue +1
- Eigenvector |{0, 1}> with eigenvalue -1
This means that, per the postulates of QM, immediately after measuring the vertical spin of an electron, the state vector of the system is either |{1, 0}> or |{0, 1}>.

The Horizontal Spin Magnet

A horizontal spin magnet measures the spin of an electron along the horizontal axis:
An electron enters the port on the left and exits one of the two ports on the right. An electron exiting through the upper port hits the upper detecting screen, indicating its horizontal spin = +1. An electron exiting the lower port hits the lower detecting screen, indicating its horizontal spin = -1.
The horizontal spin magnet is represented in Quantum Mechanics by an operator whose matrix form is:
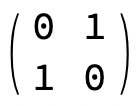
- - (This is the Pauli matrix for σ_x.)
The operator’s eigenvectors and eigenvalues are:
- Eigenvector |{1/√2, 1/√2}> with eigenvalue +1
- Eigenvector |{1/√2, -1/√2}> with eigenvalue -1
Thus, per the Collapse Postulate, immediately after measuring the horizontal spin of an electron, the state vector of the system is either |{1/√2, 1/√2}> or |{1/√2, -1/√2}>.

An Experiment with Sequential Magnets

Suppose that an electron is fed through a vertical spin magnet and, if it exits the +1 port, is fed through a second vertical spin magnet.
What happens is that the electron exits the second magnet through the +1 port as well. And that’s what QM predicts. That is, QM predicts, with probability 1, that measuring the vertical spin of an electron in state |{1, 0}> causes the system to collapse into the same state |{1, 0}>. The mathematical formulation of this prediction is:
- |<{1, 0}|{1, 0}>|² = 1.
Similarly, if the electron exits the first magnet through the -1 port and then goes through the second magnet, the electron exits through its -1 port as well.
QM predicts this happens with probability 1. That is, QM predicts that the state vector |{0, 1}> collapses into |{0, 1}> with probability = 1. Mathematically speaking:
- |<{0, 1}|{0, 1}>|² = 1
We get the same results using sequential horizontal spin magnets rather than sequential vertical spin magnets.

An Experiment with Different Sequential Magnets

Suppose an electron is fed through a horizontal spin magnet and, if it exits the +1 port, is then fed into a vertical spin magnet.
QM predicts that the probability of the electron exiting the +1 port of the vertical spin magnet is 1/2 and that the probability of it exiting the -1 port is likewise 1/2. That is, QM predicts that the state vector |{1/√2, 1/√2}> collapses into |{1, 0}> with probability 1/2 and collapses into |{0, 1}> with probability 1/2. In mathematical terms:
- |<{1/√2, 1/√2}|{1, 0}>|² = 1/2
- |<{1/√2, 1/√2}|{0, 1}>|² = 1/2
And that’s what’s observed when lots of electrons are fed through the magnets. That is, approximately half the electrons exit through the +1 port of the vertical magnet and approximately half the electrons exit through the -1 port.
- (Frequencies verify probabilities.)
And the results are the same if the electron exits the -1 port of the horizontal magnet rather than the +1 port.
And, finally, the results are the same when the magnets are reversed. For example:
That is, QM predicts that the state vector |{1, 0}> collapses into |{1/√2, 1/√2}> with probability 1/2 and collapses into |{1/√2, -1/√2}> also with probability 1/2.
- |<{1, 0} | {1/√2, 1/√2}>|² = 1/2
- |<{1, 0} | {1/√2, -1/√2}>|² = 1/2

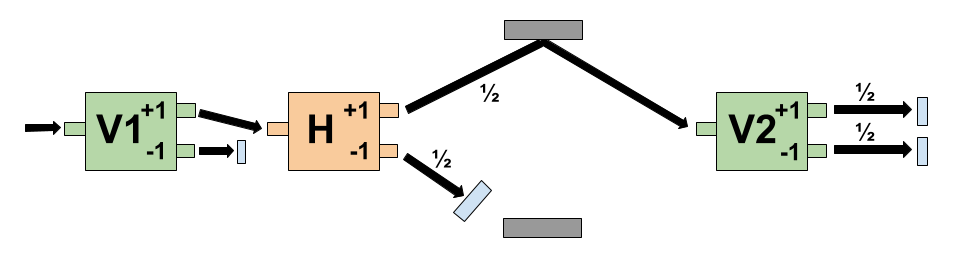
The Two-Path Experiment

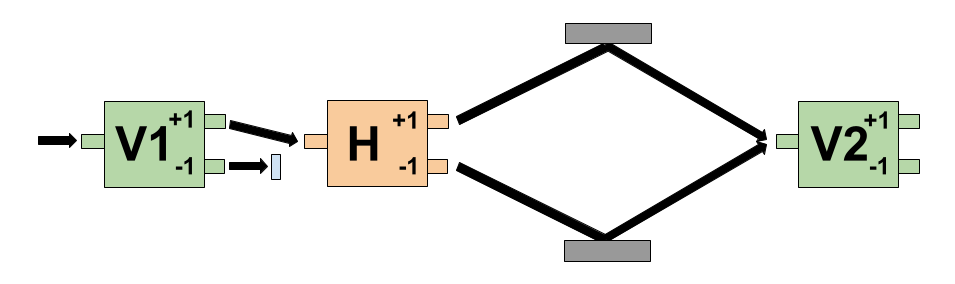
The Two-Path Experiment consists of a horizontal spin magnet sandwiched between two vertical spin magnets.
An electron is fed into the V1 magnet and, if it exits the +1 port, is then fed into the horizontal magnet H. An electron exiting the +1 port of the H magnet is reflected off a mirror (which doesn’t affect its spin) and then enters the V2 magnet on the right. An electron exiting the -1 port of the H magnet is reflected off a different mirror and then enters the V2 magnet.
Quantum Mechanics predicts that the electron exits the +1 port of the V2 magnet with probability = 1.
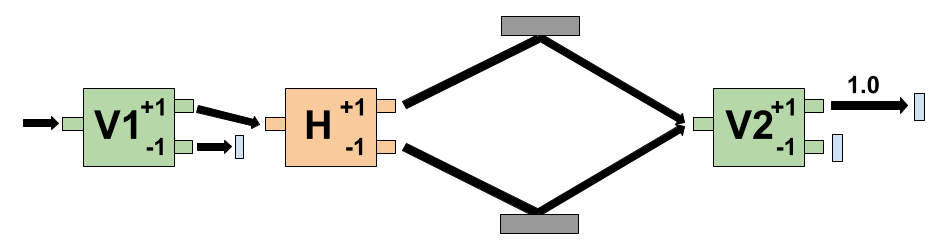
And that’s what’s observed. That is, when lots of electrons are fed through the system, all of them emerge from the +1 port of the V2 magnet.
But this seems to conflict with the earlier finding that, for an electron that enters a vertical spin magnet from a horizontal spin magnet, the probability that it exits the +1 port of the vertical spin magnet is 1/2 and the probability that it exits the -1 port is also 1/2.
Indeed, here’s a deductive argument that seems to prove that the V2 probabilities are 1/2 and 1/2:
1. The state of the system as the electron passes between V1 and H = |{1, 0}>.
2. The state of the system as the electron passes between H and V2 is either |{1/√2, 1/√2}> or |{1/√2, -1/√2}>.
3. If state of the system as the electron passes between H and V2 is |{1/√2, 1/√2}>, then the probability that the electron exits V2 through the +1 port is 1/2 and the probability that it exits V2 through the -1 port is 1/2. That’s because the state vector |{1/√2, 1/√2}> collapses into |{1, 0}> with probability 1/2 and collapses into |{0, 1}> with probability 1/2. Mathematically that’s:
  - |<{1/√2, 1/√2}|{1, 0}>|² = 1/2
  - |<{1/√2, 1/√2}|{0, 1}>|² = 1/2
4. If state of the system as the electron passes between H and V2 is |{1/√2, -1/√2}>, then the probability that the electron exits V2 through the +1 port is 1/2 and the probability that it exits V2 through the -1 port is 1/2. That’s because the state vector |{1/√2, -1/√2}> collapses into |{1, 0}> with probability 1/2 and collapses into |{0, 1}> with probability 1/2. Mathematically that’s:
  - |<{1/√2, -1/√2}|{1, 0}>|² = 1/2
  - |<{1/√2, -1/√2}|{0, 1}>|² = 1/2
5. Therefore, an electron entering the V1 magnet exits the V2 magnet either through the +1 port with probability 1/2 or through the -1 port with probability 1/2.
One of the premises of this argument is false.

Let’s consider a modification of the experiment in which one of the paths between the H and V2 magnets is blocked.
Quantum Mechanics predicts that an electron entering the H magnet
- exits the -1 port of H with probability 1/2
- exits the +1 port of V2 with probability 1/4
  - = 1/2 x 1/2
- exits the -1 port of V2 with probability 1/4
  - = 1/2 x 1/2.
This makes perfect sense.

So what’s going with the Two-Path Experiment when the electron has two open paths from H to V2?
First, recall the Collapse Postulate:
- If an observable (with operator M) is measured with outcome λ, the state vector |ψ⟩ of the system immediately after the measurement is the eigenvector of M with eigenvalue λ.
Second, note that when one of the paths from H to V2 is blocked three measurements take place: the first by magnet V1, the second by magnet H, and the third by magnet V2.
But — and this is the key fact — only two measurements take place when there are two open paths from H to V2: the first by V1, the second by V2. No measurement takes place at H. Hence, per the Collapse Postulate, the state vector collapses only twice. The first collapse is right after the measurement by V1, which makes the state vector = |{1, 0}>. Magnet H and the mirrors have no effect on the state vector. So, the second collapse, at V2, is simply the collapse of |{1, 0}> into itself. Thus, the two-path configuration amounts to nothing more than two sequential vertical magnets:
And the problem with the deductive argument, which seemed to show that QM’s prediction was wrong, is that the second premise is false. That is, it’s false that:
- The state of the system as the electron passes between H and V2 is either |{1/√2, 1/√2}> or |{1/√2, -1/√2}>.
The state of the system as the electron passes between H and V2 is in fact = |{1, 0}>.

Sources

Britannica Article on the Philosophy of Physics (David Z Albert)
Quantum Mechanics and Experience, David Z Albert
Quantum Mechanics: The Theoretical Minimum, Leonard Susskind & Art Friedman