Probability

Outline

Probability Theory

Probability Theory is the formal theory of probability
Developed in 1654 by French mathematicians Pierre de Fermat and Blaise Pascal, Probability Theory is used in physics, genetics, statistics, the social sciences, decision theory, investment analysis, actuarial forecasting, risk assessment, and blocking spam.
These pages set forth basic probability theory by solving seven problems of increasing difficulty. The last is the infamous Monty Hall problem, gotten wrong by hundreds of PhDs.

Seven Problems

Aces and Hearts
- What’s the probability of randomly picking the ace of hearts from a standard deck of 52 cards?
- Also, what are the probabilities of selecting an ace, a heart, an ace or a heart, neither ace nor heart, a red or black card, a black heart?
- View Aces and Hearts
Flipping Coins
- A normal coin is randomly flipped three times in a row; what’s the probability of three heads?
- Three coins are tossed simultaneously; what’s the probability of three heads?
- View Flipping Coins
With and Without Replacement
- Three cards are randomly selected from a standard deck. What’s the probability they’re all hearts given that the cards are selected:
  - Consecutively with replacement
  - Consecutively without replacement
  - Simultaneously
- View With and Without Replacement
Sixes
- Three dice are tossed. What’s the probability of rolling:
  - Three sixes
  - At least one six
  - Exactly one six
- View Sixes
Cell Phones and Day Packs
- Among 1,000 students 400 have cell phones (C), 300 daypacks (D), and 350 neither. What are the following probabilities for a randomly selected student: P(C&D), P(~C&~D), P(C), P(D), P(CvD), P(~C), P(D|C), P(C|D).
- View Cell Phones and Day Packs
Random Drug Test
- You’re given a random drug test that’s 95 percent reliable, meaning 95 percent of drug users test positive and 95 percent of non-drug users test negative. Assume five percent of the population takes drugs. You test positive. What’s the probability you use drugs?
- View Random Drug Test
Monty Hall
- You’re a contestant on a game show and asked to choose one of three closed doors. Behind one door is the car of your dreams; behind the others, goats. You pick a door, Door 1, say, and the host, knowing what’s behind each door, opens one of the other doors, Door 3 for example, revealing a goat. (He always opens a door with a goat.) He then gives you the option of changing your selection to Door 2. Do you have a better chance of winning if you switch; or are the odds the same?
- View Monty Hall

Conditional Probability

Conditional probability is the probability of something given that something else is the case.
Notation
- “P(….. | —–) = n” means that the probability that ….. given that —– equals n.
The probability of randomly drawing a King from a standard deck of 52 cards is 4/52 = 1/13
- That is, P(King) = 1/13
But the probability of drawing a King given that the card is a Face Card is 1/3, since there are 4 Kings and 12 Face Cards.
- That is, P(King | Face Card) = 1/3, where “|” means “given that.”
The formal definition of conditional probability is
- P(A|B) = P(A&B) / P(B), where P(B) > 0
Thus, P(King | Face Card) = P(King & Face Card) / P(Face Card) = (4/52) / (12/52) = 4/12 = 1/3.
P(A|B) is not P(B|A)
- P(King | Face Card) = 1/3
- But P(Face Card | King) = 1

Probability Rules

Probability Tools

Calculators
- Random Drug Test
Natural Frequencies
- Random Drug Test
Possibility Trees
- Flipping Coins
Possibility Tables
- Flipping Coins
- Sixes
Probability Rules
- All Problems
Probability Trees
- Random Drug Test
Probability Tables
- Cell Phones and Day Packs
- Random Drug Test
Venn Diagrams

Bayes Theorem

The core idea of Bayes Theorem is that the probability of a hypothesis given the evidence is, in part, a function of the probability of the evidence given the hypothesis.

View Bayes Theorem

Mendel’s Theory of Heredity

Mendel’s Theory uses probability theory to make predictions

View Mendel’s Theory of Heredity

Evidential Probability

The evidential probability of a proposition is the degree to which it’s supported by the evidence and arguments.

View Evidential Probability

Evidential Arguments

View Evidential Arguments

Axioms, Definitions, Theorems

Tautology
- If A is a tautology, P(A) = 1
- Status: Axiom
Equivalence
- If A and B are logically equivalent, P(A) = P(B)
- Status: Axiom
Special Disjunctive Rule
- P(A∨B) = P(A) + P(B), where A and B are logically incompatible
- Status: Axiom
Contradiction
- If A is a contradiction, P(A) = 0
- Status: Theorem
  - Derivation
    - Let B be a tautology and A any contradiction. Then:
    - P(B) = 1
      - Tautology
    - Since A v B follows from B, A v B is also a tautology. Therefore:
    - P(A v B) = 1
      - Tautology
    - P(A) + P(B) = 1
      - Special Disjunctive Rule
    - P(A) + 1 = 1
      - Since P(B) = 1
    - P(A) = 0
      - Subtract 1 from both sides
Negation Rule
- P(~A) = 1 – P(A)
- Status: Theorem
  - Derivation
    - P(A v ~A) = 1
      - Tautology
    - P(A) + P(~A) = 1
      - Special Disjunctive Rule
    - P(~A) = 1 – P(A)
      - Subtract P(~A) from both sides
General Disjunctive Rule
- P(A v B) = P(A) + P(B) – P(A&B)
- Status: Theorem
  - Derivation
    - P(A) = P(A&B) + P(A&~B)
      - Equivalence
    - P(B) = P(A&B) + P(~A&B)
      - Equivalence
    - P(A) + P(B) = 2 P(A&B) + P(A&~B) + P(~A&B)
      - Add the two equations
    - P(A) + P(B) – P(A&B) = P(A&B) + P(A&~B) + P(~A&B)
      - Subtract P(A&B) from both sides
    - P(A) + P(B) – P(A&B) = P(A v B)
      - Equivalence
        
        A v B is equivalent to A&B v A&~B v ~A&B
Conditional Probability
- P(A|B) =df P(A&B) / P(B), where P(B) > 0
- Status: Definition
Independence
- A and B are independent =df P(A|B) = P(A)
- Status: Definition
General Conjunction Rule
- P(A&B) = P(A|B) x P(B)
- Status: Theorem
  - Derivation
    - P(A|B) = P(A&B) / P(B)
      - Conditional Probability
    - P(A&B) = P(A|B) x P(B)
      - Multiply both sides by P(B)
Special Conjunction Rule
- P(A&B) = P(A) x P(B), if A and B are independent
- Status: Theorem
  - Derivation
    - P(A&B) = P(A|B) x P(B)
      - General Conjunction Rule
    - P(A&B) = P(A) x P(B)
      - Independence
Bayes Theorem (Non-Comparative Form)
- P(A|B) = P(A) P(B|A) / P(B)
- Status: Theorem
  - Derivation
    - P(A|B) = P(A&B) / P(B)
      - Conditional Probability
    - P(A|B) = P(A) P(B|A) / P(B)
      - General Conjunction Rule
Bayes Theorem (Comparative Form, Single Hypothesis)
- P(A|B) = P(A) P(B|A) /( P(A) P(B|A) + P(~A) P(B|~A) )
- Status: Theorem
  - Derivation
    - P(A|B) = P(A&B) / P(B)
      - Conditional Probability
    - P(A|B) = P(A&B) / P((B&A) v (B&~A))
      - Equivalence
        
        B is logically equivalent to B&A v B&~A
    - P(A|B) = P(A&B) /( P(B&A) + P(B&~A) )
      - Special Disjunction Rule
    - P(A|B) = P(A) P(B|A) /( P(A) P(B|A) + P(~A) P(B|~A) )
      - General Conjunction Rule

Theorems for Venn Diagrams

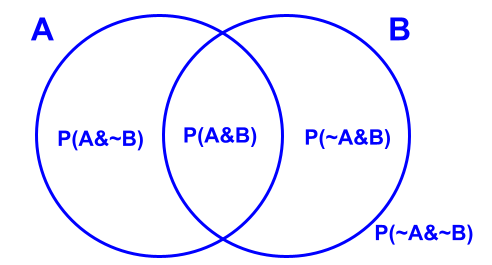
Theorem for P(A)
- P(A) = P(A&B) + P(A&~B)
- Derivation
  - P(A) = P(A&B v A&~B)
    - Equivalence
      - A is logically equivalent to A&B v A&~B
  - P(A) = P(A&B) + P(A&~B)
    - Special Disjunction Rule
Theorem for P(B)
- P(B) = P(A&B) + P(~A&B)
- Derivation
  - P(B) = P(A&B v ~A&B)
    - Equivalence
      - B is logically equivalent to A&B v ~A&B
  - P(B) = P(A&B) + P(~A&B)
    - Special Disjunction Rule
Theorem for Venn Diagram Partition of Sample Space
- P(A&B) + P(A&~B) + P(~A&B) + P(~A&~B) = 1
- Derivation
  - P(A&B v A&~B v ~A&B v ~A&~B) = 1
    - Tautology
  - P(A&B) + P(A&~B) + P(~A&B) + P(~A&~B) = 1
    - Special Disjunction Rule
Theorem for P(A|B)
- P(A|B) = P(A&B) / (P(A&B) + P(~A&B))
- Derivation
  - P(A|B) = P(A&B) / P(B)
    - Conditional Probability
  - P(B) = P(A&B) + P(~A&B)
    - Theorem for P(B)
  - P(A|B) = P(A&B) / (P(A&B) + P(~A&B))
    - Replace P(B) with P(A&B) + P(~A&B)